1:
a: Xét ΔOBA và ΔOCA có
OB=OC
AB=AC
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}\)
mà \(\widehat{OBA}=90^0\)
nên \(\widehat{OCA}=90^0\)
=>AC\(\perp\)OC tại C
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔBCE nội tiếp
BE là đường kính
Do đó: ΔBCE vuông tại C
=>BC\(\perp\)CE tại C
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
Ta có: OA\(\perp\)BC
CE\(\perp\)CB
Do đó: OA//CE
2: Gọi giao điểm của EC với BA là K
Ta có: BC\(\perp\)CE tại C
=>BC\(\perp\)EK tại C
=>ΔBCK vuông tại C
Ta có: \(\widehat{ACK}+\widehat{ACB}=\widehat{BCK}=90^0\)
\(\widehat{AKC}+\widehat{ABC}=90^0\)(ΔBCK vuông tại C)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ACK}=\widehat{AKC}\)
=>AC=AK
mà AC=AB
nên AK=AB(3)
Ta có: CH\(\perp\)BE
BA\(\perp\)BE
Do đó: CH//BA
Xét ΔEBA có MH//BA
nên \(\dfrac{MH}{BA}=\dfrac{EM}{EA}\left(4\right)\)
Xét ΔEAK có MC//AK
nên \(\dfrac{MC}{AK}=\dfrac{EM}{EA}\left(5\right)\)
Từ (3),(4),(5) suy ra MH=MC
=>M là trung điểm của CH
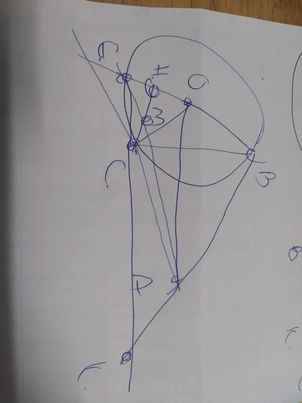











 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ







