Bài 1:
a: Xét ΔABC và ΔAMN có
\(\widehat{ABC}=\widehat{AMN}\)(hai góc so le trong, BC//MN)
AB=AM
\(\widehat{BAC}=\widehat{MAN}\)(hai góc đối đỉnh)
Do đó: ΔABC=ΔAMN
b: ΔABC=ΔAMN
=>AC=AN
=>A là trung điểm của CN
Bài 2:
a: Xét ΔOAB có
OC là đường cao
OC là đường phân giác
Do đó: ΔOAB cân tại O
=>OA=OB
b: Xét ΔOAD và ΔOBD có
OA=OB
\(\widehat{AOD}=\widehat{BOD}\)
OD chung
Do đó: ΔOAD=ΔOBD
=>DA=DB
Bài 3:
a: Xét ΔAKH và ΔACB có
AK=AC
\(\widehat{KAH}=\widehat{CAB}\)(hai góc đối đỉnh)
AH=AB
Do đó: ΔAKH=ΔACB
=>\(\widehat{AKH}=\widehat{ACB}\)
=>KH//BC
b: Xét ΔAKD và ΔACE có
\(\widehat{AKD}=\widehat{ACE}\)
AK=AC
\(\widehat{KAD}=\widehat{CAE}\)(hai góc đối đỉnh)
Do đó: ΔAKD=ΔACE
=>AD=AE
mà D,A,E thẳng hàng
nên A là trung điểm của DE
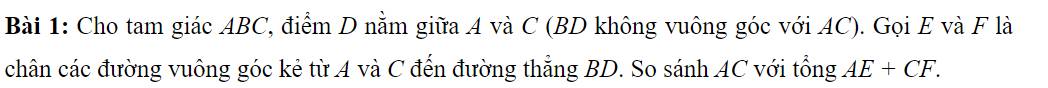
vẽ hình luôn giúp em ạ
Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé
