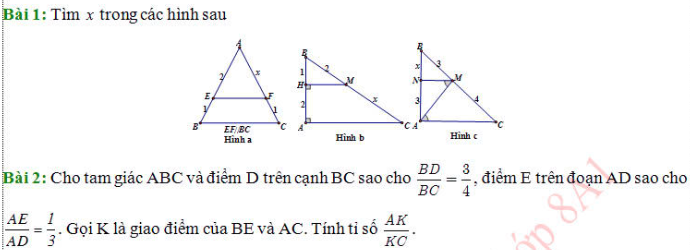
Bài 1:
a: Xét ΔABC có EF//BC
nên \(\dfrac{AE}{EB}=\dfrac{AF}{FC}\)
=>\(\dfrac{x}{1}=\dfrac{2}{1}\)
=>x=2
b: Ta có: HM\(\perp\)BA
AB\(\perp\)AC
Do đó:HM//AC
Xét ΔBAC có HM//AC
nên \(\dfrac{BM}{MC}=\dfrac{BH}{HA}\)
=>\(\dfrac{1}{2}=\dfrac{2}{x}\)
=>x=4
c: Ta có: \(\widehat{NMA}=\widehat{MAC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên NM//AC
Xét ΔBAC có NM//AC
nên \(\dfrac{BM}{MC}=\dfrac{BN}{NA}\)
=>\(\dfrac{x}{3}=\dfrac{3}{4}\)
=>x=2,25
Bài 2: Kẻ DH//BK(H\(\in\)KC)
Ta có: \(\dfrac{BD}{BC}=\dfrac{3}{4}\)
=>\(BD=\dfrac{3}{4}BC\)
Ta có: BD+CD=BC
=>\(CD=BC-\dfrac{3}{4}BC=\dfrac{1}{4}BC\)
=>\(\dfrac{CD}{DB}=\dfrac{\dfrac{1}{4}BC}{\dfrac{3}{4}BC}=\dfrac{1}{4}:\dfrac{3}{4}=\dfrac{1}{3}\)
Xét ΔBKC có DH//BK
nên \(\dfrac{CH}{CK}=\dfrac{CD}{CB}=\dfrac{1}{4}\) và \(\dfrac{CD}{DB}=\dfrac{CH}{HK}=\dfrac{1}{3}\)
CH/HK=1/3
=>CH=1/3HK
Xét ΔADH có EK//DH
nên \(\dfrac{AE}{AD}=\dfrac{AK}{AH}\)
=>\(\dfrac{AK}{AH}=\dfrac{1}{3}\)
=>\(\dfrac{AK}{KH}=\dfrac{1}{2}\)
=>AK=1/2KH
AK+KH+HC=AC
=>\(AC=KH+\dfrac{1}{2}KH+\dfrac{1}{3}HK=\dfrac{11}{6}HK\)
Ta có: AK+KC=AC
=>\(\dfrac{1}{2}KH+KC=\dfrac{11}{6}KH\)
=>KC=8/6KH=4/3KH
\(\dfrac{AK}{KC}=\dfrac{1}{2}:\dfrac{4}{3}=\dfrac{1}{2}\cdot\dfrac{3}{4}=\dfrac{3}{8}\)