Question

  vẽ giúp hình bài này với

Answer 1

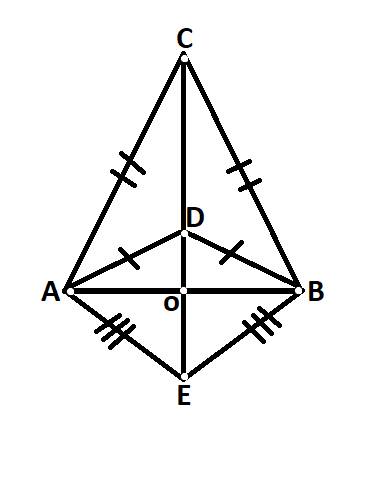
a: Ta có: \(AE=EB=\dfrac{AB}{2}\)

\(AD=DC=\dfrac{AC}{2}\)

mà AB=AC

nên AE=EB=AD=DC

Xét ΔADB và ΔAEC có

AD=AE

\(\widehat{DAB}\) chung

AB=AC

Do đó: ΔADB=ΔAEC

=>BD=CE
b: Xét ΔEBC và ΔDCB có

EB=DC

BC chung 

EC=DB

Do đó: ΔEBC=ΔDCB

=>\(\widehat{ECB}=\widehat{DBC}\)

=>\(\widehat{GBC}=\widehat{GCB}\)

Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)

nên ΔGBC cân tại G

c:

Xét ΔABC có

E,D lần lượt là trung điểm của AB,AC

=>ED là đường trung bình của ΔABC

=>\(ED=\dfrac{1}{2}BC\)

Xét ΔGED có GE+GD>ED

mà \(ED=\dfrac{1}{2}BC\)

nên \(GE+GD>\dfrac{1}{2}BC\)