Đồ thị hàm số \(y=\sqrt{2}x\)
+) Đi qua gốc tọa độ O(0;0)
+) Đi qua điểm A \(\left(1;\sqrt{2}\right)\)
Vẽ đồ thị hs:
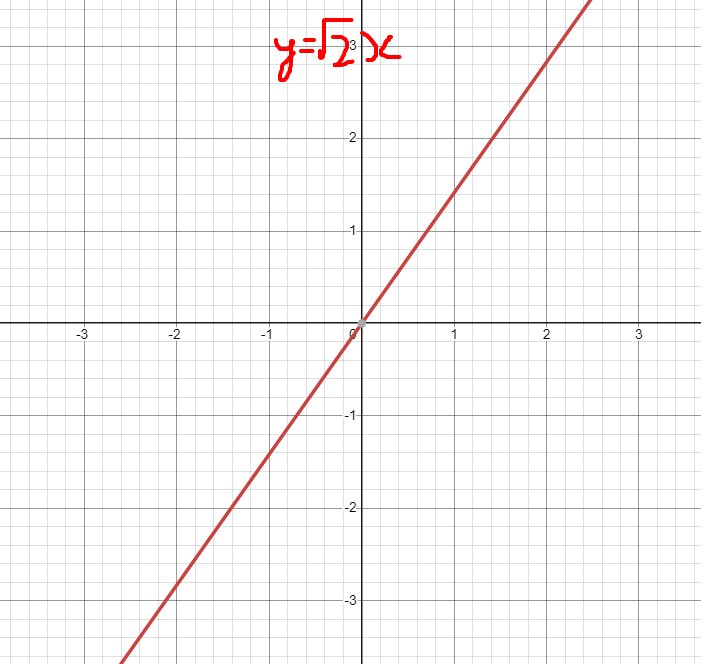
Đồ thị hàm số \(y=\sqrt{2}x\)
+) Đi qua gốc tọa độ O(0;0)
+) Đi qua điểm A \(\left(1;\sqrt{2}\right)\)
Vẽ đồ thị hs:
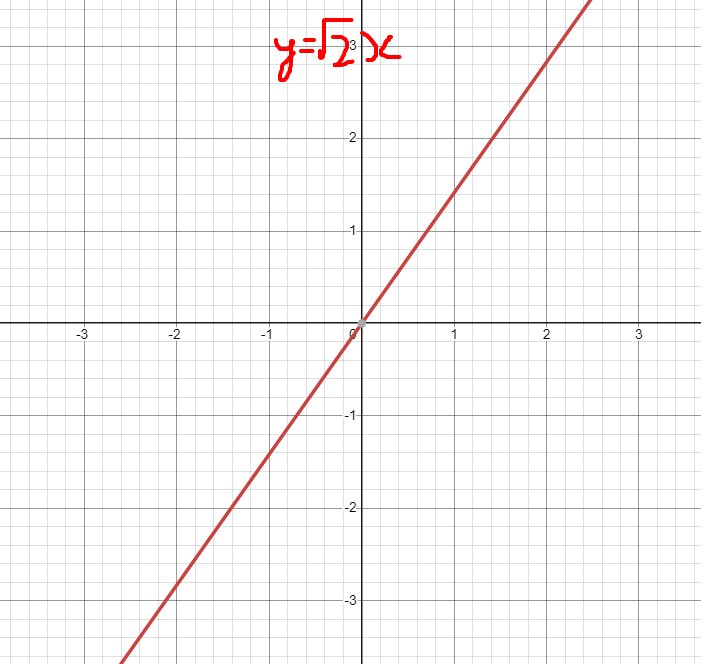
Cho hàm số \(y=\sqrt{x^2-4x+4}-\sqrt{x^2+4x+4}\)
a) Vẽ đồ thị hàm số
b) Dùng đồ thị tìm giá trị max của y, giá trị min của y
Cho hàm số \(y=\sqrt{x^2-4x+4}-\sqrt{x^2+4x+4}\)
a) Vẽ đồ thị hàm số
b) Dùng đồ thị hàm số tìm giá trị max của y, giá trị min của y
Bài 1: Giải phương trình
a) \(\sqrt{x^2+4x+4}=2\)
b) \(\sqrt{4x-8}-7\sqrt{\dfrac{x-2}{49}}=5\)
Bài 2: Trong mặt phẳng tọa độ Oxy:
a) Vẽ đồ thị (d₁) của hàm số y = \(-\dfrac{1}{2}x+\dfrac{3}{2}\)
b) Gọi A và B là giao điểm của đồ thị (d₁) với các trục tọa độ. Tính diện tích ∆OAB (với O là gốc tọa độ)
Bài 3: Rút gọn
A= \(\dfrac{2\sqrt{x}-4}{3\sqrt{x}-4}+\dfrac{x+22\sqrt{x}-32}{3x-10\sqrt{x}+8}+\dfrac{4+2\sqrt{x}}{\sqrt{x}-2}\:\left(x\:\ge0;\:x\ne4;\:x\ne\dfrac{16}{9}\right)\)
Vẽ đồ thị hàm số và nêu cách vẽ biết
y=\(\sqrt{8}\)x
y=\(\sqrt{11}\)x
vẽ đồ thị hàm số y= \(\sqrt{3}\)x+3
Vẽ đồ thị của hàm số: \(y=\sqrt{x}\)
P/s: Dạo
Cho hàm số y=3x
a) Vẽ đồ thị hàm số
b) Điểm A thuộc đồ thị hàm số có khoảng cách tới gốc tọa độ là \(2\sqrt{10}\). Xác định tọa độ của A.
cho hàm số y =\(\sqrt{x^2+\sqrt{x^2+4x+4}}\)
1. tìm tập xác định của hàm số
2. rút gọn y( loại bỏ dấu căn và dấu giá trị tuyệt đối)
3. vẽ đồ thị hàm số
Cho hàm số y = - 3x + 2 (d) a) Vẽ đồ thị (d) của hàm số trên. b) Tìm m để đồ thị hàm số y = (m+1)x - 3 song song với đồ thị hàm số y = - 3x + 2.