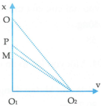
Trong một thí nghiệm về giao thoa sóng nước, hai nguồn kết hợp O 1 và O 2 dao động cùng pha, cùng biên độ. Chọn hệ trục tọa độ vuông góc xOy thuộc mặt nước với gốc tọa độ là vị trí đặt nguồn O 1 còn nguồn O 2 nằm trên trục Oy. Hai điểm P và Q nằm trên Ox có OP = 4,5 cm và OQ = 8 cm. Dịch chuyển nguồn O 2 trên trục Oy đến vị trí sao cho góc P O 2 Q có giá trị lớn nhất thì phần tử nước tại P không dao động còn phần tử nước tại Q dao động với biên độ cực đại. Biết giữa P và Q không còn cực đại nào khác. Trên đoạn OP, điểm gần P nhất mà các phần tử nước dao động với biên độ cực đại cách P một đoạn là:
A. 3,4 cm.
B. 2,0 cm.
C. 2,5 cm.
D. 1,1 cm.
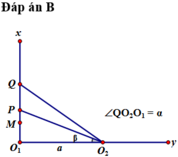
Có tan P O 2 Q = tan α - β = tan α - tan β 1 + tan α . tan β = 8 a - 4 ٫ 5 a 1 + 8 a . 4 ٫ 5 a = 3 ٫ 5 a + 36 a
Áp dụng BĐT Cauchy cho mẫu, ta tìm được
tan P O 2 Q ≤ 3 ٫ 5 12 ⇒ P O 2 Q m a x ⇔ a = 6 c m .
Q là cực đại, P là cực tiểu gần nguồn hơn và gần Q nhất nên ta có :
Q O 2 - Q O 1 = k λ P O 2 - P O 1 = k + 0 ٫ 5 λ ⇔ k λ = 2 k + 0 ٫ 5 λ = 3 ⇔ λ = 2 c m k = 1
Gọi M là cực đại gần P nhất. Vì Q là cực đại với k = 1 nên M là cực đại với k = 2.
⇒ M O 2 - M O 1 = 2 λ = 4 ⇒ M O 1 2 + 36 - M O 1 = 4 ⇔ M O 1 = 2 ٫ 5 c m
Suy ra PM = 4,5 – 2,5 = 2 (cm).