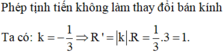Các câu hỏi tương tự
Trong mặt phẳng (Oxy), cho (C’) là ảnh của đường tròn (C)
x
−
1
2
+
y
−
2
2
100
qua phép vị tự tâm O tỉ số k 1/2 Xác định tâm I và...
Đọc tiếp
Trong mặt phẳng (Oxy), cho (C’) là ảnh của đường tròn (C) x − 1 2 + y − 2 2 = 100 qua phép vị tự tâm O tỉ số k = 1/2 Xác định tâm I' và bán kính R' của (C')?
A. I ' = 1 2 ; 1 ; R ' = 5 .
B. I ' = 2 ; 4 ; R ' = 20 .
C. I ' = − 1 ; 1 2 ; R ' = 5 .
D. I ' = − 4 ; 2 ; R ' = 20 .
Trong mặt phẳng Oxy, cho đường tròn
C
:
x
+
1
2
+
y
-
2
2
4
. Viết phương trình đường tròn ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số...
Đọc tiếp
Trong mặt phẳng Oxy, cho đường tròn
C : x + 1 2 + y - 2 2 = 4 . Viết phương trình đường tròn ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 2 và phép tịnh tiến theo vectơ v = ( 1;2 ).
A. x - 3 2 + y - 6 2 = 16
B. x - 3 2 + y - 6 2 = 4
C. x - 1 2 + y - 2 2 = 16
D. x - 1 2 + y - 2 2 = 4
Trong mặt phẳng tọa độ Oxy cho đường tròn tâm I(2;-2), bán kính R 4. Viết phương trình đường tròn là ảnh của đường tròn (I;R) qua phép vị tự tâm O, tỉ số
1
2
. A.
x
-
4
2
+
(
y
+
4
)
2
4
B. ...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho đường tròn tâm I(2;-2), bán kính R = 4. Viết phương trình đường tròn là ảnh của đường tròn (I;R) qua phép vị tự tâm O, tỉ số 1 2 .
A. x - 4 2 + ( y + 4 ) 2 = 4
B. x - 4 2 + ( y + 4 ) 2 = 64
C. x - 1 2 + ( y + 1 ) 2 = 4
D. x - 1 2 + ( y + 1 ) 2 = 64
Trong mặt phẳng tọa độ Oxy cho đường tròn
C
:
x
-
6
2
+
y
-
4
2
12
. Viết phương trình đường tròn là ảnh của đường tròn (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số
k...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho đường tròn C : x - 6 2 + y - 4 2 = 12 . Viết phương trình đường tròn là ảnh của đường tròn (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 1 2 và phép quay tâm góc 90 °
A. x + 2 2 + y - 3 2 = 6
B. x - 2 2 + y + 3 2 = 6
C. x + 2 2 + y - 3 2 = 3
D. x + 2 2 + y - 3 2 = 9
Trong mặt phẳng tọa độ Oxy, cho đường tròn
C
:
x
2
+
y
2
+
2
x
-
4
y
+
1
0
. Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ sốk 2 có phương trình là A.
x
2
+
y
2
+
4
x
-
8
y...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn C : x 2 + y 2 + 2 x - 4 y + 1 = 0 . Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ số
k = 2 có phương trình là
A. x 2 + y 2 + 4 x - 8 y + 4 = 0
B. x 2 + y 2 - 4 x + 8 y + 4 = 0
C. x 2 + y 2 + 4 x - 8 y - 4 = 0
D. x 2 + y 2 + 4 x - 8 y + 2 = 0
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C):
(
x
+
1
)
2
+
(
y
-
3
)
2
4
. Phép tịnh tiến theo vectơ
v
→
3
;
2
biến đường tròn (C) thành đường tròn có phương trình nào dưới đây A.
(...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): ( x + 1 ) 2 + ( y - 3 ) 2 = 4 . Phép tịnh tiến theo vectơ v → = 3 ; 2 biến đường tròn (C) thành đường tròn có phương trình nào dưới đây
A. ( x + 2 ) 2 + ( y + 5 ) 2 = 4
B. ( x - 1 ) 2 + ( y + 3 ) 2 = 4
C. ( x + 4 ) 2 + ( y - 1 ) 2 = 4
D. ( x - 2 ) 2 + ( y - 5 ) 2 = 4
Trong mặt phẳng Oxy, cho đường thẳng d có phương trình x+y-10 và đường tròn (C):
(
x
-
3
)
2
+
(
y
-
1
)
2
1
. Ảnh của đường thẳng d qua phép tịnh tiến theo véc tơ
v
→
4
;
0
cắt đường tròn (C) tại hai điểm...
Đọc tiếp
Trong mặt phẳng Oxy, cho đường thẳng d có phương trình x+y-1=0 và đường tròn (C): ( x - 3 ) 2 + ( y - 1 ) 2 = 1 . Ảnh của đường thẳng d qua phép tịnh tiến theo véc tơ v → = 4 ; 0 cắt đường tròn (C) tại hai điểm A x 1 ; y 1 và B x 2 ; y 2 . Giá trị x 1 + x 2 bằng
A. 5
B. 8
C. 6
D. 7
Cho đường tròn (C) có tâm I(1;2) và bán kính
R
3
. Phép tịnh tiến theo vecto
v
→
2
;
0
biến (C) thành (C’) có phương trình là A.
x
−
3
2
+
y
−...
Đọc tiếp
Cho đường tròn (C) có tâm I(1;2) và bán kính R = 3 . Phép tịnh tiến theo vecto v → 2 ; 0 biến (C) thành (C’) có phương trình là
A. x − 3 2 + y − 2 2 = 9
B. x − 1 2 + y + 2 2 = 9
C. x + 3 2 + y + 2 2 = 9
D. x − 3 2 + y − 2 2 = 3
Cho mặt cầu
S
:
x
2
+
y
2
+
z
2
4
a
2
. Mặt cầu (S) cắt mặt phẳng (Oxy) theo đường tròn (C). Tìm tọa độ tâm J và tính bán kính r của đường tròn (C). A. J(0;0;0), r 4a B. J(0;0;0), r 2a C. J(1;1;0), r 2a D. J(1;1;1), r 2a
Đọc tiếp
Cho mặt cầu S : x 2 + y 2 + z 2 = 4 a 2 . Mặt cầu (S) cắt mặt phẳng (Oxy) theo đường tròn (C). Tìm tọa độ tâm J và tính bán kính r của đường tròn (C).
A. J(0;0;0), r = 4a
B. J(0;0;0), r = 2a
C. J(1;1;0), r = 2a
D. J(1;1;1), r = 2a