Question

trong mặt phẳng tọa độ Oxy cho 2 hàm số y=-x^2/2 và y=x/2-1

a)vẽ đồ thị của 2 hàm số này trên cùng 1 mặt phảng tọa độ

b)Tìm tọa đồ giao điểm của 2 đồ thị đó

Answer 1

Lời giải:

a.

b.

PT hoành độ giao điểm:

$\frac{-x^2}{2}=\frac{x}{2}-1$

$\Leftrightarrow -x^2=x-2$

$\Leftrightarrow x^2+x-2=0$

$\Leftrightarrow (x-1)(x+2)=0$

$\Leftrightarrow x-1=0$ hoặc $x+2=0$

$\Leftrightarrow x=1$ hoặc $x=-2$
Với $x=1$ thì $y=\frac{x}{2}-1=\frac{1}{2}-1=\frac{-1}{2}$. Ta có giao điểm thứ nhất $(1,\frac{-1}{2})$

Với $x=-2$ thì $y=\frac{x}{2}-1=\frac{-2}{2}-1=-2$. Ta có giao điểm thứ hai $(-2,-2)$

Answer 2

a)

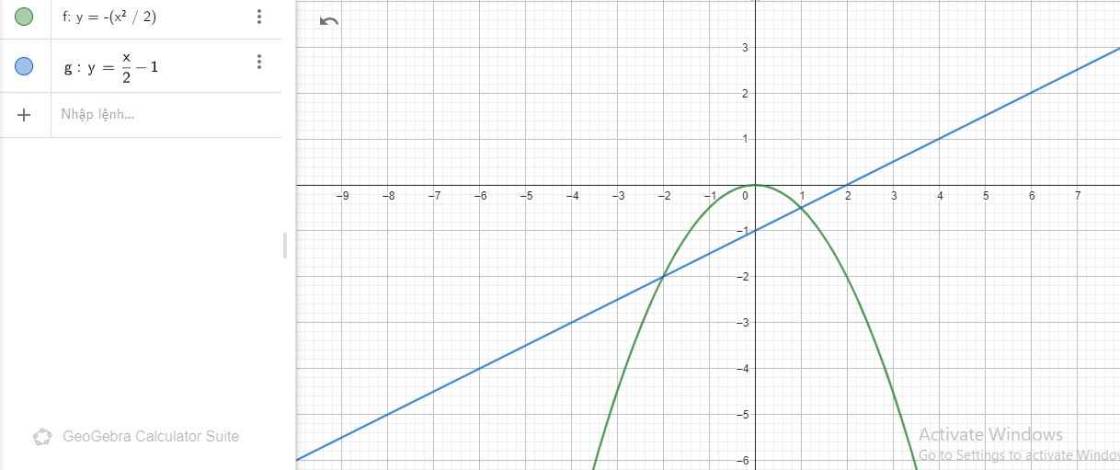
b)

Xét PT hoành độ giao điểm \(y=-\dfrac{x^2}{2}\) và \(y=\dfrac{x}{2}-1\) có

\(-\dfrac{x^2}{2}=\dfrac{x}{2}-1\Leftrightarrow\dfrac{x^2}{2}+\dfrac{x}{2}-1=0\Leftrightarrow x^2+x-2=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

Thay x=1 vào \(y=\dfrac{x}{2}-1\) có:

\(y=\dfrac{1}{2}-1=-\dfrac{1}{2}\)

Thay x= -2 vào \(y=\dfrac{x}{2}-1\) có

\(y=\dfrac{-2}{2}-1=-1-1=-2\)

Vậy 2 đồ thị hàm số trên cắt nhau tại 2 điểm \(\left(1;-\dfrac{1}{2}\right)\) và \(\left(-2;-2\right)\)