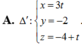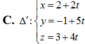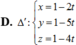Question

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình  x 2 + y 2 + z 2 = 9 và điểm M(1;-1;1). Mặt phẳng (P) đi qua M và cắt (S) theo giao tuyến là đường tròn có chu vi nhỏ nhất có phương trình là:

A. x-y+z-1=0

A. x-y+z-1=0

C. x-y+z-3=0

D. x+y+z-1=0

Answer 1

Đáp án C

Phương pháp:

Kiểm tra M nằm trong hay ngoài mặt cầu.

Để giao tuyến là đường tròn có chu vi nhỏ nhất thì bán kính của đường tròn đó là nhỏ nhất  là lớn nhất  

Cách giải:

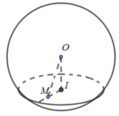
x 2 + y 2 + z 2 = 9 có tâm O(0;0;0) 

Nhận xét: Dễ dàng kiểm tra điểm M nằm trong (S), do đó, mọi mặt phẳng đi qua M luôn cắt (S) với giao tuyến là 1 đường tròn.

Để giao tuyến là đường tròn có chu vi nhỏ nhất thì bán kính của đường tròn đó là nhỏ nhất.  là lớn nhất.

Mà  lớn nhất khi M trùng I hay OM vuông góc với (P) 

Vậy, (P) là mặt phẳng qua M và có VTPT là  

Phương trình mặt phẳng (P) là: