Đáp án C
Xét S : x - 1 2 + y + 2 2 + z - 3 2 = 16 có tâm I(1;-2;3), bán kính R = 4
Chu vi đường tròn giao tuyến 4 π 3 = 2 πr ⇔ r = 2 3
Khi đó d I ; P = R 2 - r 2 = 4 2 - 2 3 2 = 2 ⇔ m - 6 3 = 2 ⇒ [ m = 12 m = 0
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz cho
S
:
x
2
+
y
2
+
z
2
-
2
x
+
4
z
-
11
0
là phương trình mặt cầu và
α
:
x
+
y
-
z
+
3
0
là ph...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho S : x 2 + y 2 + z 2 - 2 x + 4 z - 11 = 0 là phương trình mặt cầu và α : x + y - z + 3 = 0 là phương trình mặt phẳng . Biết mặt cầu S cắt mặt phẳng α theo giao tuyến là đường tròn T . Chu vi của đường tròn T bằng
A. π
B. 2 π
C. 4 π
D. 6 π
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+y+z+m 0 (m là tham số) và mặt cầu (S):
(
x
-
2
)
2
+
(
y
+
1
)
2
+
z
2
16
. Tìm các giá trị của m để (P) cắt (S) theo giao tuyến là đường tròn có bán kính lớn nhất. A.
-
1
-
4
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+y+z+m= 0 (m là tham số) và mặt cầu (S): ( x - 2 ) 2 + ( y + 1 ) 2 + z 2 = 16 . Tìm các giá trị của m để (P) cắt (S) theo giao tuyến là đường tròn có bán kính lớn nhất.
A. - 1 - 4 3 ≤ m ≤ - 1 + 4 3 .
B. m ≠ 0 .
C. m =1.
D. m = -1
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
(
P
)
:
x
−
y
+
2
z
+
1
0
và
(
Q
)
:
2
x
+
y
+
z
−
z
0.
Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán k...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( P ) : x − y + 2 z + 1 = 0 và ( Q ) : 2 x + y + z − z = 0. Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính r. Xác định r sao cho chỉ có duy nhất một mặt cầu (S) thỏa mãn điều kiện bài toán
A. r = 3 2 2 .
B. r = 10 2 .
C. r = 3 .
D. r = 14 2 .
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) tâm I(1;2;3) và mặt phẳng (P): 2x-y-2z+120. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có chu vi
6
π
.Viết phương trình mặt cầu A.
(
x
-
1
)
2
+
(
y
-
2
)...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) tâm I(1;2;3) và mặt phẳng (P): 2x-y-2z+12=0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có chu vi 6 π .Viết phương trình mặt cầu
A. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 8
B. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 13
C. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9
D. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 12
Trong không gian tọa độ Oxyz, cho mặt cầu (S): (x-2)2 + y2 + (z+1)2 9 và mặt phẳng (P): 2x-y-2z-30. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính R của (C).
Đọc tiếp
Trong không gian tọa độ Oxyz, cho mặt cầu (S): (x-2)2 + y2 + (z+1)2 = 9 và mặt phẳng (P): 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính R của (C).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
(
P
)
:
2
x
−
2
y
−
z
−
9
0
và mặt cầu
(
S
)
:
(
x
−
3
)
2
+
(
y
+
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : 2 x − 2 y − z − 9 = 0 và mặt cầu ( S ) : ( x − 3 ) 2 + ( y + 2 ) 2 + ( z − 1 ) 2 = 100 . Biết (P) cắt (S) theo giao tuyến là một đường tròn. Tìm tọa độ tâm của đường tròn giao tuyến.
A. (3;2;-1)
B. (-3;2;-1)
C. (3;-2;1)
D. (-3;2;1)
Trong không gian tọa độ Oxyz, cho mặt cầu (S) có phương trình (x-2)2 + (y+1)2 + (z-3)2 20. Mặt phẳng có phương trình x-2y+2z-10 và đường thẳng
∆
có phương trình
x
1
y
+
2
2
z
+
4
-
30
.
Viết phương trình đường thẳng ...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho mặt cầu (S) có phương trình (x-2)2 + (y+1)2 + (z-3)2 = 20. Mặt phẳng có phương trình x-2y+2z-1=0 và đường thẳng ∆ có phương trình x 1 = y + 2 2 = z + 4 - 30 . Viết phương trình đường thẳng ∆ ' nằm trong mặt phẳng α vuông góc với ∆ đồng thời cắt (S) theo một dây cung có độ dài lớn nhất.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
α
có phương trình.
2
x
+
2
y
−
z
−
8
0.
Xét mặt cầu
S
:
x
2
+
y
2
+
z
2
−
2
x
+
4
y
−
z
+...
Đọc tiếp
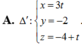
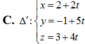
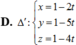
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng α có phương trình. 2 x + 2 y − z − 8 = 0. Xét mặt cầu S : x 2 + y 2 + z 2 − 2 x + 4 y − z + m = 0 , với m là tham số thực. Biết mặt phẳng α cắt mặt cầu (S) theo giao tuyến là một đường tròn (C) có bán kính bằng 2. Tìm tất cả các giá trị của m thỏa mãn điều kiện trên.
A. m = − 18
B. m = 21 4
C. m = 27 2
D. m = − 11
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) và mặt phẳng (P) có phương trình lần lượt là
S
:
x
2
+
y
2
+
z
2
−
2
x
+
4
y
−
6
z
−
11
0
và
P
:
2
x
+
2
y...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) và mặt phẳng (P) có phương trình lần lượt là S : x 2 + y 2 + z 2 − 2 x + 4 y − 6 z − 11 = 0 và P : 2 x + 2 y − z + 17 = 0 . Viết phương trình mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) theo một giao tuyến là đường tròn có chu vi bằng 6 π
A. Q : 2 x + 2 y − z = 0
B. Q : 2 x + 2 y − z + 5 = 0
C. Q : 2 x + 2 y − z − 2 = 0
D. Q : 2 x + 2 y − z − 7 = 0