Đáp án B
Phương pháp: Sử dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau:
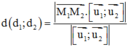
Với ![]() lần lượt là các VTCP của
lần lượt là các VTCP của ![]()
Cách giải:
Ta có ![]() lần lượt là các VTCP của d1; d2
lần lượt là các VTCP của d1; d2
Ta có ![]()
Lấy ![]()
![]()
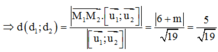
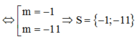
Đáp án B
Phương pháp: Sử dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau:
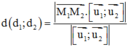
Với ![]() lần lượt là các VTCP của
lần lượt là các VTCP của ![]()
Cách giải:
Ta có ![]() lần lượt là các VTCP của d1; d2
lần lượt là các VTCP của d1; d2
Ta có ![]()
Lấy ![]()
![]()
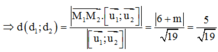
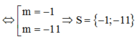
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y - 1 2 = z - 1 1 ; d 2 : x 1 = y + 1 2 = z - 6 - 5 . gọi A là giao điểm của d 1 v à d 2 ; d là đường thẳng qua điểm M (2; 3;1) cắt d 1 , d 2 lần lượt tại B, C sao cho B C = 6 A B . Tính khoảng cách từ O đến đường thẳng d, biết rằng d không song song với mặt phẳng (Oxz)
A. 10 5
B. 10 3
C. 13
D. 10
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng chéo nhau ∆ : x - 2 2 = y - 3 - 4 = z - 1 - 5 và d : x - 1 1 = y - 2 = z + 1 2 . Khoảng cách giữa hai đường thẳng ∆ và d bằng
A. 5 5
B. 45 14
C. 5
D. 3
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y + 1 2 + z 2 = 11 và hai đường thẳng d 1 : x − 5 1 = y + 1 1 = z − 1 2 ; d 2 : x + 1 1 = y 2 = z 1 . Viết phương trình tất cả các mặt phẳng tiếp xúc với mặt cầu (S) đồng thời song song với hai đường thẳng d 1 , d 2
A. α : 3 x − y − z − 15 = 0
B. α : 3 x − y − z + 7 = 0
C. α : 3 x − y − z − 7 = 0
D. α : 3 x − y − z + 7 = 0 hoặc α : 3 x − y − z − 15 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y + 1 ) 2 + z 2 = 11 và hai đường thẳng d 1 : x - 5 1 = y + 1 1 = z - 1 2 , d 2 : x + 1 1 = y 2 = z 1 . Phương trình tất cả các mặt phẳng tiếp xúc với mặt cầu ( S ) đồng thời song song với hai đường thẳng d 1 , d 2
A. 3 x - y - z - 7 = 0
B. 3 x - y - z - 7 = 0 v à 3 x - y - z - 15 = 0
C. 3 x - y - z + 7 = 0
D. 3 x - y - z - 15 = 0
Trong không gian với hệ tọa độ Oxyz cho ba đường thẳng d 1 : x = t y = 4 − t z = − 1 + 2 t , d 2 : x 1 = y − 2 − 3 = z − 3 v à d 3 : x + 1 5 = y − 1 2 = z + 1 1 . Gọi ∆ là đường thẳng cắt d 1 , d 2 , d 3 lần lượt tại các điểm A, B, C sao cho AB = BC. Phương trình đường thẳng ∆ là
A. x − 2 1 = y − 2 1 = z 1
B. x 1 = y − 2 1 = z 1
C. x 1 = y − 3 1 = z − 1 − 1
D. x 1 = y − 3 − 1 = z − 1 1
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y - 1 1 = z + 1 1 và d 2 : x + 1 2 = y - 1 - 1 = z 2 . Đường thẳng qua điểm M(1;1;1) và cắt d 1 , d 2 lần lượt tại A, B. Tính tỉ số MA/MB.
A. M A M B = 3 2 .
B. M A M B = 2.
C. M A M B = 1 2 .
D. M A M B = 2 3 .
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S
A. 36 2 π
B. 18 π
C. 36 π
D. 18 2 π
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 = x - 1 1 = y - 1 1 = z + 1 1 và d 2 = x + 1 2 = y - 1 - 1 = z 2 Đường thẳng qua điểm M 1 ; 1 ; 1 và cắt d1, d2 lần lượt tại A, B. Tính tỉ số M A M B
A. M A M B = 3 2 .
B. M A M B = 2 .
C. M A M B = 1 2 .
D. M A M B = 2 3 .
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ : x + 1 2 = y 3 = z + 1 − 1 và hai điểm A 1 ; 2 ; − 1 , B 3 ; − 1 ; − 5 . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Khi đó, gọi M a ; b ; c là giao điểm của d với đường thẳng Δ . Giá trị P = a + b + c bằng
A. -2
B. 4
C. 2
D. 6