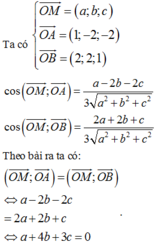
Vậy tập hợp các điểm M thỏa mãn yêu cầu bài toán thuộc mặt phẳng x + 4 y + 3 z = 0
Chọn A.
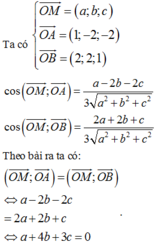
Vậy tập hợp các điểm M thỏa mãn yêu cầu bài toán thuộc mặt phẳng x + 4 y + 3 z = 0
Chọn A.
Trong không gian Oxyz cho hai điểm A(1;1;2) và B(1;3;-1) và mặt phẳng (P) có phương trình x - 2y - z + 1 = 0. M là điểm trên mặt phẳng (P) thỏa mãn MA + MB đạt giá trị nhỏ nhất. Tọa độ điểm M là
A. M 3 2 ; 1 ; 1 2 .
B. M − 3 2 ; 1 ; − 5 2 .
C. M 1 ; 1 ; 0 .
D. Không có M
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( α ) : bc . x + ac . y + ab . z - abc = 0 với a, b, c là các số khác 0 thỏa mãn 1 a + 2 b + 3 c = 7 . Gọi A, B, C lần lượt là giao điểm của α với các trục tọa độ Ox, Oy, Oz. Biết mặt phẳng α tiếp xúc với mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 72 7 . Thể tích khối OABC với O là gốc tọa độ bằng
A. 2 9
B. 3 4
C. 1 8
D. 4 3
Trong không gian với hệ tọa độ Oxyz có bao nhiêu mặt phẳng song song với mặt phẳng Q : x + y + z + 3 = 0 , cách điểm M(3;2;1) một khoảng bằng 3 3 biết rằng tồn tại một điểm X(a;b;c) trên mặt phẳng đó thỏa mãn a + b + c < − 2 ?
A. 1
B. Vô số
C. 2
D. 0
Trong không gian với hệ tọa độ Oxyz có bao nhiêu mặt phẳng song song với mặt phẳng (Q): x + y + z + 3 = 0 cách điểm M(3;2;1) một khoảng bằng 3 3 biết rằng tồn tại một điểm X(a,b,c) trên mặt phẳng đó thỏa mãn a + b + c < –2?
A. 2
B. 1
C. Vô số
D. 0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : m x + ( m + 1 ) y − z − 2 m − 1 = 0 , với m là tham số. Gọi (T) là tập hợp các điểm H m là hình chiếu vuông góc của điểm H ( 3 ; 3 ; 0 ) trên (P). Gọi a, b lần lượt là khoảng cách lớn nhất, khoảng cách nhỏ nhất từ O đến một điểm thuộc (T). Khi đó, a + b bằng
A. 5 2 .
B. 3 3 .
C. 8 2 .
D. 4 2 .
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;3) và đường thẳng d có phương trình x - 1 2 = y - 2 - 1 = z z . Mặt phẳng chứa A và d. Viết phương trình mặt cầu tâm O tiếp xúc với mặt phẳng (P).
A. x 2 + y 2 + z 2 = 12 5 .
B. x 2 + y 2 + z 2 = 3 .
C. x 2 + y 2 + z 2 = 6 .
D. x 2 + y 2 + z 2 = 24 5 .
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(–1; –2;0), B(0; –4;0), C(0;0; –3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A. (P): 6x – 3y + 5z = 0
B. (P): 6x – 3y + 4z = 0
C. (P): 2x – y – 3z = 0
D. (P): 2x – y + 3z = 0
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm O(0;0;0), A(0;1;-2), B(1;2;1), C(4;3;m). Giá trị m để 4 điểm O, A, B, C đồng phẳng là
A. -7
B. -14
C. 14
D. 7
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A 1 ; 0 ; − 3 , B − 3 ; − 2 ; − 5 . Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức A M 2 + B M 2 = 30 là một mặt cầu (S), tọa độ tâm I và bán kính R của mặt cầu (S) là
A. I − 2 ; − 2 ; − 8 , R = 3
B. I − 1 ; − 1 ; − 4 , R = 6
C. I − 1 ; − 1 ; − 4 , R = 3
D. I − 1 ; − 1 ; − 4 , R = 30 2