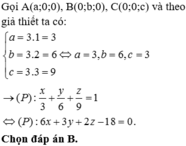Các câu hỏi tương tự
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C. Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC. A.
x
1
+
y
2
+
z
3
3
B.
6
x
+
3
y
−
2
z
−
6
0
C. ...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C. Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. x 1 + y 2 + z 3 = 3
B. 6 x + 3 y − 2 z − 6 = 0
C. x + 2 y + 3 z − 14 = 0
D. x + 2 y + 3 z − 11 = 0
Trong không gian Oxyz cho điểm M(1;2;3). Phương trình mặt phẳng (P) đi qua M cắt các trục tọa độ Ox; Oy; Oz lần lượt tại A, B, C sao cho M là trong tâm của tam giác ABC là
A. (P):6x + 3y + 2z + 18 = 0
B. (P):6x + 3y + 2z + 6 = 0
C. (P):6x + 3y + 2z - 18 = 0
D. (P):6x + 3y + 2z - 6 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho điểm G(1;2;3). Mặt phẳng đi qua G cắt Ox, Oy, Oz lần lượt tại A, B, C sao cho G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng
α
A.
α
:
x
2
+
y
4
+
z
6
1
B.
α
:
x...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm G(1;2;3). Mặt phẳng đi qua G cắt Ox, Oy, Oz lần lượt tại A, B, C sao cho G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng α
A. α : x 2 + y 4 + z 6 = 1
B. α : x 3 + y 2 + z 1 = 1
C. α : x 1 + y 2 + z 3 = 1
D. α : x 3 + y 6 + z 9 = 1
Trong không gian Oxyz cho điểm
M
1
;
2
;
3
. Viết phương trình mặt phẳng (P) đi qua M cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C sao cho M là trọng tâm của tam giác ABC. A.
P
:
6
x
+
3
y
+
2
z
+
18
0
...
Đọc tiếp
Trong không gian Oxyz cho điểm M 1 ; 2 ; 3 . Viết phương trình mặt phẳng (P) đi qua M cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C sao cho M là trọng tâm của tam giác ABC.
A. P : 6 x + 3 y + 2 z + 18 = 0
B. P : 6 x + 3 y + 2 z + 6 = 0
C. P : 6 x + 3 y + 2 z - 18 = 0
D. P : 6 x + 3 y + 2 z - 6 = 0
Trong không gian Oxyz cho điểm
M
1
;
2
;
3
. Viết phương trình mặt phẳng
P
đi qua M cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C sao cho M là trọng tâm của tam giác ABC. A.
P
:
6
x
+
3
y
+
2
z
+
18
0
B.
P...
Đọc tiếp
Trong không gian Oxyz cho điểm M 1 ; 2 ; 3 . Viết phương trình mặt phẳng P đi qua M cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C sao cho M là trọng tâm của tam giác ABC.
A. P : 6 x + 3 y + 2 z + 18 = 0
B. P : 6 x + 3 y + 2 z + 6 = 0
C. P : 6 x + 3 y + 2 z - 18 = 0
D. P : 6 x + 3 y + 2 z - 6 = 0
Trong không gian Oxyz, cho hai điểm
M
1
;
2
;
3
,
A
2
;
4
;
4
và hai mặt phẳng
Q
:
x
-
2
y
-
z
+
4
0
,
P...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm M 1 ; 2 ; 3 , A 2 ; 4 ; 4 và hai mặt phẳng Q : x - 2 y - z + 4 = 0 , P : x + y - 2 z + 1 = 0 . Đường thẳng ∆ đi qua điểm M, cắt hai mặt phẳng P , Q lần lượt tại B và C a ; b ; c sao cho tam giác ABC cân tại A và nhận AM làm đường trung tuyến. Tính T = a + b + c .
A. T = 9
B. T = 3
C. T = 7
D. T = 5
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm
M
1
;
2
;
3
và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC. A.
6
x
+
3
y
−
2
z
−
6
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm M 1 ; 2 ; 3 và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 6 x + 3 y − 2 z − 6 = 0
B. x + 2 y + 3 z − 14 = 0
C. x + 2 y + 3 z − 11 = 0
D. x 1 + y 2 + z 3 = 3
Trong không gian với hệ toạ độ Oxyz, cho điểm M(4;3;2). Có bao nhiêu mặt phẳng qua M cắt ba trục toạ độ Ox,Oy,Oz lần lượt tại A,B,C sao cho 6OA=2OB=3OC>0.
A. 8.
B. 1.
C. 3.
D. 4.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
+
2
y
+
3
z
0
. Các điểm A, B, C lần lượt là giao điểm (khác gốc tọa độ) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phư...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x + 2 y + 3 z = 0 . Các điểm A, B, C lần lượt là giao điểm (khác gốc tọa độ) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là