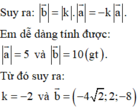Đáp án A
Do vectơ
b
→
ngược hướng với
a
→
nên
b
→
=
k
.
a
→
, k < 0.