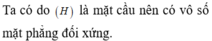Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng
Δ
:
x
1
x
+
3
1
z
2
. Biết rằng mặt cầu (S) có bán kính bằng
2
2
và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính bằng 2. Tìm tọa độ tâm I A. I(1;-2;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng Δ : x 1 = x + 3 1 = z 2 . Biết rằng mặt cầu (S) có bán kính bằng 2 2 và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính bằng 2. Tìm tọa độ tâm I
A. I(1;-2;2), I(5;2;10)
B. I(1;-2;2), I(0;-3;0)
C. I(5;2;10), I(0;-3;0)
D. I(1;-2;2), I(-1;2;-2)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng
(
α
)
:
x
1
,
(
β
)
:
y
-
1
,
(
γ
)
:
z
1
. Bán kính của mặt cầu (S) bằng A.
33
B. 1 C.
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng ( α ) : x = 1 , ( β ) : y = - 1 , ( γ ) : z = 1 . Bán kính của mặt cầu (S) bằng
A. 33
B. 1
C. 3 2
D. 3
Trong không gian Oxyz cho đường thẳng
d
:
x
-
1
y
-
2
1
z
-
3
2
và hai mặt phẳng
α
:
x
+
2
y
+
2
z
+
1
0
,
β
:
2
x
-...
Đọc tiếp
Trong không gian Oxyz cho đường thẳng d : x - 1 = y - 2 1 = z - 3 2 và hai mặt phẳng α : x + 2 y + 2 z + 1 = 0 , β : 2 x - y - 2 z + 7 = 0 . Mặt cầu (S) có tâm nằm trên đường thẳng d và (S) tiếp xúc với hai mặt phẳng α và β có bán kính là:
A. 2 ∨ 12
B. 4 ∨ 144
C. 2 ∨ 2 3
D. 2 ∨ 2
Trong không gian Oxyz cho đường thẳng
d
:
x
-
1
y
-
2
1
z
-
3
2
và hai mặt phẳng
α
:
x
+
2
y
+
2
z
+
1
0
,
β
:
2
x
-...
Đọc tiếp
Trong không gian Oxyz cho đường thẳng d : x - 1 = y - 2 1 = z - 3 2 và hai mặt phẳng α : x + 2 y + 2 z + 1 = 0 , β : 2 x - y - 2 z + 7 = 0 . Mặt cầu (S) có tâm nằm trên đường thẳng d và (S) tiếp xúc với hai mặt phẳng α và β có bán kính là:
A. 2 ∨ 12
B. 4 ∨ 144
C. 2 ∨ 2 3
D. 2 ∨ 2
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng A.
V
πa
3
24
B.
V
πa
3
3
C.
V
πa
3
6
D.
V
4
3...
Đọc tiếp
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng
A. V = πa 3 24
B. V = πa 3 3
C. V = πa 3 6
D. V = 4 3 πa 3
Cho hình chóp
S
.
A
B
C
D
có SA vuông góc với mặt phẳng (ABC), đáy ABC là tam giác cân tại A và
B
A
C
^
120
°
,
B
C
2
a
. Gọi M. N lần lượt là hình chiếu của điểm A trên SB, SC. Tính bán kính mặt cầu đi qua bốn điểm A, N, M, B. A. ...
Đọc tiếp
Cho hình chóp S . A B C D có SA vuông góc với mặt phẳng (ABC), đáy ABC là tam giác cân tại A và B A C ^ = 120 ° , B C = 2 a . Gọi M. N lần lượt là hình chiếu của điểm A trên SB, SC. Tính bán kính mặt cầu đi qua bốn điểm A, N, M, B.
A. 2 a 3 3
B. 2 a 3
C. a 3 2
D. a 3
Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm A(1;2;1); B(3;2;3) , có tâm thuộc mặt phẳng (P):x-y-3=0, đồng thời có bán kính nhỏ nhất, hãy tính bán kính R thuộc mặt cầu (S)?
A. 1
B. 2
C. 2
D. 2 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
2
2
, cạnh bên SA vuông góc với mặt phẳng đáy và SA3 Mặt phẳng
α
qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP. A.
V
64
2
π
3
B.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA=3 Mặt phẳng α qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP.
A. V = 64 2 π 3
B. V = 125 π 6
C. V = 32 π 3
D. V = 10 Sπ 3
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
2
1
y
+
3
2
z
-
1
3
. Viết phương trình đường thẳng d’ là hình chiếu vuông góc của d lên mặt phẳng (Oyz). A.
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 2 1 = y + 3 2 = z - 1 3 . Viết phương trình đường thẳng d’ là hình chiếu vuông góc của d lên mặt phẳng (Oyz).
A. d ' : x = 0 y = 3 + 2 t z = 0
B. d ' : x = 2 + t y = - 3 + 2 t z = 0
C. d ' : x = 0 y = - 3 + 2 t z = 1 + 3 t
D. d ' : x = t y = 2 t z = 0