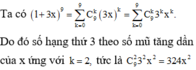Các câu hỏi tương tự
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Biết rằng khi khai triển nhị thức Niutơn
x
+
1
2
x
4
n
a
0...
Đọc tiếp
Biết rằng khi khai triển nhị thức Niutơn x + 1 2 x 4 n = a 0 x n + a 1 x n - 1 . 1 x 4 + a 2 x n - 2 . 1 x 4 2 + a 3 x n - 3 . 1 x 4 3 . . . (với n là số nguyên lớn hơn 1) thì ba số a 0 , a 1 , a 2 theo thứ tự lập thành một cấp số cộng. Hỏi trong khai triển trên, có bao nhiêu số hạng mà lũy thừa của x là một số nguyên.
A. 1
B. 2
C. 3
D. 4
Gọi
a
2018
là hệ số của số hạng chứa
x
2018
trong khai triển nhị thức Niutơn
x
−
x
n
với
x
≥
0
; n là số nguyên dương thỏa mãn
1
2
!
.2017
!...
Đọc tiếp
Gọi a 2018 là hệ số của số hạng chứa x 2018 trong khai triển nhị thức Niutơn x − x n với x ≥ 0 ; n là số nguyên dương thỏa mãn 1 2 ! .2017 ! + 1 4 ! .2015 ! + 1 6 ! .2013 ! ... + 1 2016 ! .3 ! + 1 2018 ! = 2 2018 − 1 P n . Tìm a 2018
A. 2017
B. − C 2018 3 .
C. 2019
D. C 2019 2 .
Trong khai triển nhị thức
2
x
8
16
+
32
16
2
x
m
, cho số hạng thứ tư tr...
Đọc tiếp
Trong khai triển nhị thức 2 x 8 16 + 32 16 2 x m , cho số hạng thứ tư trừ số hạng thứ sáu bằng 56, hệ số của số hạng thứ ba trừ hệ số của số hạng thứ 2 bằng 20. Giá trị của x là
A. -1
B. 2
C. 1
D. -2
Cho nhị thức
x
+
1
x
n
,
x
≠
0
trong tổng số các hệ số của khai triển nhị thức đó là 1024. Khi đó số hạng không chứa x trong khai triển nhị thức đã cho bằng A. 252 B. 125 C. -252 D. 525
Đọc tiếp
Cho nhị thức x + 1 x n , x ≠ 0 trong tổng số các hệ số của khai triển nhị thức đó là 1024. Khi đó số hạng không chứa x trong khai triển nhị thức đã cho bằng
A. 252
B. 125
C. -252
D. 525
Tổng các hệ số nhị thức Niu – tơn trong khai triển
(
1
+
x
)
3
n
bằng 64. Số hạng không chứa x trong khai triển
(
2
n
x
+
1
...
Đọc tiếp
Tổng các hệ số nhị thức Niu – tơn trong khai triển ( 1 + x ) 3 n bằng 64. Số hạng không chứa x trong khai triển ( 2 n x + 1 2 n x 2 ) 3 n là
A. 360
B. 210
C. 250
D. 240
Cho n là số nguyên dương thỏa mãn
A
n
+
3
3
-
6
C
n
+
1
3
294
Tìm số hạng mà tích số mũ của x và y bằng 18 trong khai triển nhị thức Newton:
6
n
....
Đọc tiếp
Cho n là số nguyên dương thỏa mãn A n + 3 3 - 6 C n + 1 3 = 294
Tìm số hạng mà tích số mũ của x và y bằng 18 trong khai triển nhị thức Newton: 6 n . x 4 3 y + y 2 x 2 n (với x ≠ 0 ; y ≠ 0 ).
A. 160 x 9 y 2
B. 160 x 2 y 9
C. 160 x 3 y 6
D. 160 x 6 y 3
Tìm số hạng không chứa x trong khai triển nhị thức
2
x
-
1
n
n
,
∀
x
≠
0
biết n là số tự nhiên thỏa mãn
C
n
3
C
n
n
-
3
+...
Đọc tiếp
Tìm số hạng không chứa x trong khai triển nhị thức 2 x - 1 n n , ∀ x ≠ 0 biết n là số tự nhiên thỏa mãn C n 3 C n n - 3 + 2 C n 3 C n 4 C n n - 4 = 1225 .
A. -20
B. -8
C. -160
D. 160
Hệ số của trong khai triển của nhị thức Niu tơn
(
3
-
x
)
9
là A.
-
C
9
7
B.
C
9
7
C.
9
C...
Đọc tiếp
Hệ số của trong khai triển của nhị thức Niu tơn ( 3 - x ) 9 là
A. - C 9 7
B. C 9 7
C. 9 C 9 7
D. - 9 C 9 7