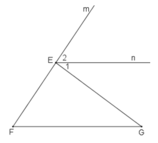
Kẻ tia En song song với FG.
∠F và ∠E2 ở vị trí đồng vị ⇒ ∠F = ∠E2. (1)
∠G và ∠E1 ở vị trí so le trong ⇒ ∠G = ∠E1. (2)
Từ (1) và (2) suy ra: ∠F + ∠G = ∠E1 + ∠E2 (đpcm).
Hay ∠EFG + ∠EGF = ∠GEm.

Kẻ tia En song song với FG.
∠F và ∠E2 ở vị trí đồng vị ⇒ ∠F = ∠E2. (1)
∠G và ∠E1 ở vị trí so le trong ⇒ ∠G = ∠E1. (2)
Từ (1) và (2) suy ra: ∠F + ∠G = ∠E1 + ∠E2 (đpcm).
Hay ∠EFG + ∠EGF = ∠GEm.
Trong hình bs 11 ta có tam giác EFG và tia Fm .
Chứng minhh rằng :
GEm = EFG + EGF
Giải giúp mình với , ai trả lời nhanh và đúng thì mình tick 5 tick cho
Trong hình 11 ta có tam giác EFG và tia Fm. Chứng minh rằng: GEm = EFG + EGF
(Hình ở SBT Toán 7; phần Ôn tập chương I; Bài tập bổ sung; bài I.2, trang 155)
Xin lỗi vì máy mình mạng yếu nên ko vẽ hình được, giúp mình nha
Các phân giác ngoài của tam giác abc cắt nhau và tạo thành tam giá efg.
a. Tính các góc cửa tam giác efg theo tam giác abc
b. Chứng minh rằng các phân giác trong của tam giác abc đi qua các đỉnh efg
Cho tam giác đều ABC có diện tích bằng 40 cm2. Ta vẽ tam giác vuông cân ACD có AC là cạnh huyền. Vẽ tiếp tam giác đều CDE. Tương tự như vậy vẽ tam giác vuông cân DEF và tam giác đều EFG. Hỏi tam giác đều EFG có diện tích bằng bao nhiêu?
help me >:
Cho tam giác EFG có EF = EG . EH là tia phân giác của góc E ( H thuộc FG )
a) Chứng minh : HF = HG
b) Chứng minh : EH vuông góc FG
cho tam giác EFG có EF=EG.Gọi M là trung điểm của FG.Chứng minh rằng EM là đường trung trực của FG
Cho tam giác ABC và tam giác EFG,biết AB=EF,AC=EG,chứng minh hai tam giác đó bằng nhau
Cho tam giác MNP=tam giác EFG biết MP=3cm;MN+NP=7cm;FG-FE=1cm. Tính chu vi tam giác EFG
Các phân giác ngoài của tam giác ABC cắt nhau tạo thành tam giác EFG. Tỉnh các góc của tam giác EFG theo các góc của tam giác ABC