Các câu hỏi tương tự
Chứng minh rằng với mọi số thực a, b, c phương trình:
(
x
–
a
)
.
(
x
-
b
)
+
(
x
-
b
)
.
(
x
-
c
)
+
(
x
–
c
)
.
(
x
-
a
)
0...
Đọc tiếp
Chứng minh rằng với mọi số thực a, b, c phương trình: ( x – a ) . ( x - b ) + ( x - b ) . ( x - c ) + ( x – c ) . ( x - a ) = 0 có ít nhất một nghiệm.
cho phương trình ax^2+bx+c=0 với các số a,b,c là các số thực nghiệm khác 0 và thỏa mãn điều kiện a+b+2c=0. Chứng minh rằng phương trình trên luôn có nghiệm trên tập số thực
Cho phương trình 3x2-c=a(x2-2x+1)-b(x-1) tìm 3 số nguyên a,b,c để phương trình có nghiệm với mọi x thược R.
Cho hàm số f(x)liên tục trên đoạn [a ; b] và f(a) b, f(b) a, với 0 a b. Khi đó phương trình nào trong các phương trình sau đây luôn có nghiệm trên khoảng (a, b). A.
f
x
+
x
2
0
B.
f
x
+
a
0
C.
f
x
-
x
0
D.
f
x
+...
Đọc tiếp
Cho hàm số f(x)liên tục trên đoạn [a ; b] và f(a) = b, f(b) = a, với 0 < a < b. Khi đó phương trình nào trong các phương trình sau đây luôn có nghiệm trên khoảng (a, b).
A. f x + x 2 = 0
B. f x + a = 0
C. f x - x = 0
D. f x + x = 0
Số các giá trị thực của tham số m để phương trình (sin x-1)(2cos^2 x - (sinx -1)(2
cos
2
x
–(2m+1)cosx+m)0 có đúng 4 nghiệm thực thuộc đoạn
0
;
2
π
là A. 1. B. 2. C. 3. D. Vô số.
Đọc tiếp
Số các giá trị thực của tham số m để phương trình (sin x-1)(2cos^2 x - (sinx -1)(2 cos 2 x –(2m+1)cosx+m)=0 có đúng 4 nghiệm thực thuộc đoạn 0 ; 2 π là
A. 1.
B. 2.
C. 3.
D. Vô số.
Chứng minh rằng với mọi tham số thực m, phương trình x6 - 65 + m.\(\sqrt[3]{2-x}\) = m(1-\(\sqrt{x-1}\) ) luôn có nghiệm.
Cho hàm số y f(x) liên tục trên
ℝ
và có đồ thị như hình Gọi m là số nghiệm của phương trình f(f(x)) 1 . Khẳng định nào sau đây là đúng? A. m 6 B. m 7 C. m 5 D. m 9
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình
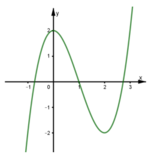
Gọi m là số nghiệm của phương trình f(f(x)) = 1 . Khẳng định nào sau đây là đúng?
A. m = 6
B. m = 7
C. m = 5
D. m = 9
Biết S(a;b) là tất cả các giá trị thực của m để phương trình
cos
3
x
-
cos
2
x
+
m
cos
x
-
1
0
có đúng 8 nghiệm thực phân biệt thuộc khoảng . Tính tổng Ta+b A. 4 B. -2 C.
17
4
D.
25
4
Đọc tiếp
Biết S=(a;b) là tất cả các giá trị thực của m để phương trình
cos
3
x
-
cos
2
x
+
m
cos
x
-
1
=
0
có đúng 8 nghiệm thực phân biệt thuộc khoảng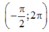 
. Tính tổng T=a+b
A. 4
B. -2
C. 17 4
D. 25 4
Cho hàm số y f(x) liên tục trên
ℝ
và có đồ thị như hình Gọi m là số nghiệm của phương trình f(f(x)) 1 . Khẳng định nào sau đây là đúng? A.
m
1
B.
m
0
C.
m
≤
0
D.
0
m
1
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình
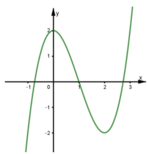
Gọi m là số nghiệm của phương trình f(f(x)) = 1 . Khẳng định nào sau đây là đúng?
A. m > 1
B. m > 0
C. m ≤ 0
D. 0 < m < 1
Tìm nghiệm âm lớn nhất của phương trình
\(\tan^{2018}x + \cot^{2018}x = 2\sin^{2017} (x+ \frac{\pi} {4})\)
có dạng \(\frac{\pi a}{b}\)với a,b là các số nguyên, a<0 và a,b nguyên tố cùng nhau. Tính S = a + b