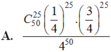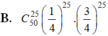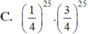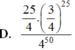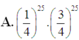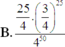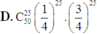Trong bài kiểm tra trắc nghiệm cuối kì, học sinh làm bài thi trắc nghiệm gồm 50 câu(mỗi câu gồm 4 phương án trả lời trong đó có 1 đáp án đúng). Bài thi được chấm theo thang điểm như sau: Mỗi câu trả lời đúng học sinh được 0,2 điểm, mỗi câu trả lời sai học sinh bị trừ 0,05 điểm. Một học sinh vì không học bài nên chọn phương án ngẫu nhiên. Tính xác suất để học sinh đó được 4,5 điểm biết học sinh đó không bỏ khoanh câu nào.
Gọi x là số câu trả lời đúng \(\Rightarrow50-x\) câu trả lời sai
Số điểm đạt được:
\(0,2.x-0,05\left(50-x\right)=4,5\)
\(\Rightarrow x=28\)
Vậy học sinh đó trả lời đúng 28 câu và trả lời sai 22 câu
Có \(C_{50}^{28}\) cách chọn 28 câu từ 50 câu
Ở mỗi câu, học sinh có \(\dfrac{1}{4}\) xác suất trả lời đúng và \(\dfrac{3}{4}\) xác suất trả lời sai
Do đó, xác suất học sinh đó được 4,5 điểm là:
\(C_{50}^{28}.\left(\dfrac{1}{4}\right)^{28}.\left(\dfrac{3}{4}\right)^{22}=...\)