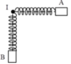
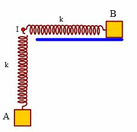
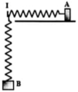
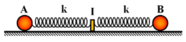
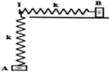
Trên mặt phẳng nằm ngang nhẵn có hai con lắc lò xo. Các lò xo có cùng độ cứng k = 50 N/m. Các vật nhỏ A và B có khối lượng lần lượt là m và 4m. Ban đầu, A và B được giữ ở hai vị trí sao cho hai lò xo đều bị giãn 8 cm. Đồng thời thả nhẹ để hai vật dao động điều hòa trên hai đường thẳng vuông góc với nhau đi qua giá I cố định (hình vẽ). Trong quá trình dao động, lực đàn hồi tác dụng lên giá I có độ lớn nhỏ nhất là:
A. 1,0 N.
B. 2,6 N.
C. 1,8 N.
D. 2,0 N.
Đáp án B
+ Lực đàn hồi tổng hợp tác dụng lên I có độ lớn
F = F 1 2 + F 2 2 = k 2 A 2 cos 2 ω t + k 2 A 2 cos 2 2 ω t = k A cos 2 ω t + cos 2 2 ω t
Biến đổi toán học
F = k A cos 2 ω t + cos 2 2 ω t = k A cos 2 ω t ⏟ x + cos 2 ω t ⏟ x - sin 2 ω t ⏟ 1 - x 2 ⏟ y
Đặt x = cos 2 ω t ⇒ y = 1 + 2 x - 1 2
+ Để F nhỏ nhất thì y nhỏ nhất
y ' = 8 x - 3 = 0 ⇔ x = 3 8 ⇒ y min = 7 16
Vậy F min = 50 . 8 . 10 - 2 7 16 ≈ 2 , 6 N .