Đáp án A
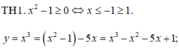
![]()
BBT1.
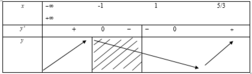
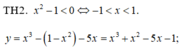
![]()
BBT2
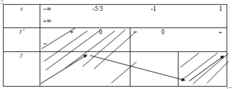
Hợp hai BBT trên ta được BBT của hàm ban đầu như sau:
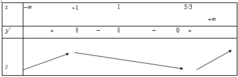
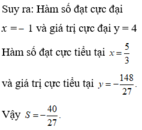
Đáp án A
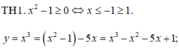
![]()
BBT1.

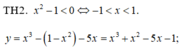
![]()
BBT2

Hợp hai BBT trên ta được BBT của hàm ban đầu như sau:

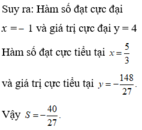
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Biết S là tập các giá trị thực của m để hàm số y = 2 f ( x ) + m có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tính tổng T = a + b.
A. T = 2
B. T = 1
C. T = -1
D. T = -2
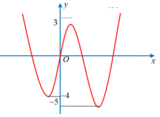
Hình vẽ bên là đồ thị của hàm số y=f(x). Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số y = f x − 1 + m có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
A. 12
B. 15
C. 18
D. 9
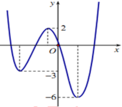
Hình vẽ bên là đồ thị của hàm số y = f(x). Gọi S là tập hợp các số nguyên dương của tham số m để hàm số y = |f(x – 1) + m| có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:
A. 12
B. 15
C. 18
D. 9
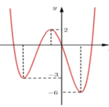
Cho hàm số y = f(x) có đồ thị như hình bên. Biết S là tập các giá trị thực của m để hàm số y = 2 f x + m có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tổng T=a+b là
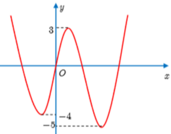
A. 2
B. 1
C. -1
D. 3
Cho đồ thị của hàm số y=f(x) như hình vẽ bên.Gọi S là tập hợp các giá trị nguyên dương của m để hàm số y = f x + 2018 + 1 3 m 2 có 5 điểm cực trị. Tổng tất cả các giá trị của các phần tử của S bằng
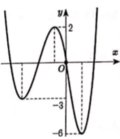
A. 7.
B. 6.
C. 5.
D. 9.
Cho hàm số y = f (x) có đồ thị như hình bên. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y = f x - 2018 + m có 5 điểm cực trị. Tổng tất cả các giá trị của tập S bằng
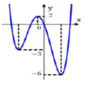
A. 9
B. 7
C. 12
D. 18
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 3 - 3 ( m + 1 ) x 2 + 6 m x có hai điểm cực trị là A và B sao cho đường thẳng AB vuông góc với đường thẳng d : y = x + 2 Số phần tử của S là
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = 2 x 3 + 3 ( m − 1 ) x 2 + 6 ( m − 2 ) x − 1 . Gọi S là tập hợp tất cả các giá trị thực của m để hàm số có hai điểm cực trị đều thuộc (-2;1). Khi đó tập S là
A. S = (1;4)
B. S = ℝ \ 3
C. S = − ∞ ; 1 ∪ 4 ; + ∞
D. S = ( 1 ; 4 ) \ 3
Hình vẽ bên là đồ thị của hàm số y=f(x). Gọi S là tập hợp các giá trị nguyên không âm của tham số m để hàm số y=|f(x-2019)+m-2| có 5 điểm cực trị. Số các phần tử của S bằng
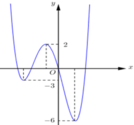
A. 3
B. 4
C. 2
D. 5
Cho hàm số f x có đạo hàm trên ℝ thỏa mãn f x + h - f x - h ≤ h 2 , ∀ x ∈ ℝ , ∀ h > 0 .Đặt g x = x + f ' x 2019 + x + f ' x 29 - m - m 4 - 29 m 2 + 100 sin 2 x - 1 , m là tham số nguyên mà m < 27. Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số g (x) đạt cực tiểu tại x = 0. Tính tổng bình phương các phần tử của S.
A. 108
B. 58
C. 100
D. 50