Các câu hỏi tương tự
Cho phương trình
2
-
m
3
-
3
m
2
+
1
.
log
81
x...
Đọc tiếp
Cho phương trình 2 - m 3 - 3 m 2 + 1 . log 81 x 3 - 3 x 2 + 1 + 2 + 2 - x 3 - 3 x 2 + 1 - 2 . log 3 1 m 3 - 3 m 2 + 1 + 2 = 0 . Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có số nghiệm thuộc đoạn 6 ; 8 . Tính tổng bình phương tất cả các phần tử của tập S.
A. 20
B. 28
C. 14
D. 10
Cho phương trình
x
3
-
3
x
2
-
2
x
+
m
-
3
+
2
2
x
3
+
3
x
+
m
3
0
. Tập S là tập hợp các giá trị của m nguyên để phương trình...
Đọc tiếp
Cho phương trình x 3 - 3 x 2 - 2 x + m - 3 + 2 2 x 3 + 3 x + m 3 = 0 . Tập S là tập hợp các giá trị của m nguyên để phương trình có ba nghiệm phân biệt. Tính tổng các phần tử của S.
A. 15.
B. 9.
C. 0.
D. 3.
Gọi S là tập hợp giá trị thực của tham số m sao cho phương trình
z
2
-
m
+
4
z
+
m
2
+
3
0
có nghiệm phức
z
0
thỏa mãn
z
0
2
. Số phần tử của tập hợp S là A. 4 B. 3 C. 2 D...
Đọc tiếp
Gọi S là tập hợp giá trị thực của tham số m sao cho phương trình z 2 - m + 4 z + m 2 + 3 = 0 có nghiệm phức z 0 thỏa mãn z 0 = 2 . Số phần tử của tập hợp S là
A. 4
B. 3
C. 2
D. 1
Gọi
z
1
,
z
2
là hai nghiệm phức của phương trình
x
3
−
3
x
2
+
4
x
−
12
0.
Tính giá trị biểu thức
P
z
1
−
z
2
.
A. 4...
Đọc tiếp
Gọi z 1 , z 2 là hai nghiệm phức của phương trình x 3 − 3 x 2 + 4 x − 12 = 0. Tính giá trị biểu thức P = z 1 − z 2 .
A. 4
B. 8
C. 2
D. 0
Cho phương trình
x
3
-
3
x
2
-
2
x
+
m
-
3
+
2
2
x
3
+
3
x
+
m
3
. Tập S là tập hợp các giá trị của m nguyên để phương trình có ba nghiệm phân...
Đọc tiếp
Cho phương trình x 3 - 3 x 2 - 2 x + m - 3 + 2 2 x 3 + 3 x + m 3 . Tập S là tập hợp các giá trị của m nguyên để phương trình có ba nghiệm phân biệt. Tính tổng các phần tử của S
A. 15.
B. 9.
C. 0.
D. 3.
Cho hàm số
y
x
3
-
3
x
2
+
3
có đồ thị như hình vẽ. Tìm tập hợp tất cả các giá trị của tham số m để phương trình
x
3
-
3
x
2
+
m
0
có ba nghiệm phân biệt A.
0
≤
m
≤
4
B. ...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 3 có đồ thị như hình vẽ. Tìm tập hợp tất cả các giá trị của tham số m để phương trình x 3 - 3 x 2 + m = 0 có ba nghiệm phân biệt
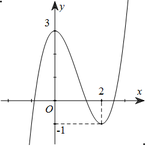
A. 0 ≤ m ≤ 4
B. - 4 ≤ m < 0
C. - 4 ≤ m ≤ 0
D. 0 < m < 4
Cho hàm số
y
−
x
3
−
3
x
2
+
2
có đồ thị hàm số như hình vẽ bên. Tìm tập hợp S tất cả các giá trị của tham số thực m sao cho phương trình
−
x
3
−
3
x
2
+
2
m
có 3 nghiệm phân biệt. A.
S
∅...
Đọc tiếp
Cho hàm số y = − x 3 − 3 x 2 + 2 có đồ thị hàm số như hình vẽ bên.
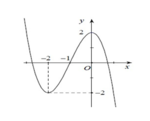
Tìm tập hợp S tất cả các giá trị của tham số thực m sao cho phương trình − x 3 − 3 x 2 + 2 = m có 3 nghiệm phân biệt.
A. S = ∅
B. S = − 2 ; 2
C. S = − 2 ; 1
D. S = − 2 ; 2
Cho hàm số
f
x
x
3
−
3
x
2
+
2
. Tập nghiệm của bất phương trình
f
x
0
là: A.
−
∞
;
0
∪
2
;...
Đọc tiếp
Cho hàm số f x = x 3 − 3 x 2 + 2 . Tập nghiệm của bất phương trình f ' x > 0 là:
A. − ∞ ; 0 ∪ 2 ; + ∞
B. 2 ; + ∞
C. − ∞ ; 0
D. 0 ; 2 .
Trên tập hợp số phức, cho phương trình
z
2
+
bz
+
c
0
với b,c
∈
ℚ
Biết rằng hai nghiệm của phương trình có dạng w + 3 và 2w – 6i +1 với w là một số phức. Tính
S
b...
Đọc tiếp
Trên tập hợp số phức, cho phương trình z 2 + bz + c = 0 với b,c ∈ ℚ Biết rằng hai nghiệm của phương trình có dạng w + 3 và 2w – 6i +1 với w là một số phức. Tính S = b 3 - c 2 .
A. S = -1841.
B. S = -3.
C. S = 7.
D. S = 2161.




