Các câu hỏi tương tự
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
Cho hình lăng trụ ABCD.ABCD có đáy là hình vuông cạnh a, cạnh bên AA2a, góc tạo bởi cạnh bên và mặt đáy bằng
60
°
. Thể tích của khối lăng trụ là
Đọc tiếp
Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình vuông cạnh a, cạnh bên AA'=2a, góc tạo bởi cạnh bên và mặt đáy bằng 60 ° . Thể tích của khối lăng trụ là
![]()
![]()
![]()
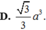
Cho hình lăng trụ ABCD.ABCD có đáy ABCD là hình thoi cạnh a, tâm O và
A
B
C
⏜
120
0
Các cạnh AA, AB, AD cùng tạo với mặt đáy một góc bằng
60
0
. Tính theo a thể tích V của khối lăng trụ đã cho.
Đọc tiếp
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và A B C ⏜ = 120 0 Các cạnh AA, A'B, A'D cùng tạo với mặt đáy một góc bằng 60 0 . Tính theo a thể tích V của khối lăng trụ đã cho.
![]()
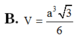
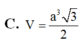
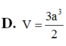
Cho hình lăng trụ đứng ABC.ABC có đáy là tam giác đều cạnh a. Cạnh bên AAa
2
. Thể tích khối lăng trụ ABC.ABC là: A.
V
a
3
6
4
B.
V...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Cạnh bên AA'=a 2 . Thể tích khối lăng trụ ABC.A'B'C' là:
A. V = a 3 6 4
B. V = a 3 6 2
C. V = a 3 6 12
D. V = a 6 4
Cho hình lăng trụ đứng ABCD.ABCD có đáy ABCD là một hình thoi cạnh a, góc BAD
60
o
Gọi M là trung điểm AA và N là trung điểm của CC Chứng minh rằng bốn điểm B, M, N, D đồng phẳng. Hãy tính độ dài cạnh AA theo a để tứ giác BMDN là hình vuông. A. a
2
B. a C.
a
2...
Đọc tiếp
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là một hình thoi cạnh a, góc BAD= 60 o Gọi M là trung điểm AA' và N là trung điểm của CC' Chứng minh rằng bốn điểm B', M, N, D đồng phẳng. Hãy tính độ dài cạnh AA' theo a để tứ giác B'MDN là hình vuông.
A. a 2
B. a
C. a 2 2
D. a 3
Cho hình lăng trụ ngũ giác ABCD.A'B'C'D'. Gọi A'', B'', C'', D'', E'' lần lượt là trung điểm của các cạnh AA', BB', CC', DD', EE'. Tỉ số thể tích giữa khối lăng trụ ABCDE.A''B''C''D''E'' và khối lăng trụ ABCDE.A'B'C'D' bằng:
A. 1/2 B. 1/4
C. 1/8 D. 1/10.
Cho hình lăng trụ đứng ABCD.ABCD có đáy là hình vuông cạnh a. Tính thể tích V của khối lăng trụ đã cho theo a, biết AB 2a. A. V
2
3
a
3
B. V a3 C. V
3
a
3
D. V
3
a
3
3
Đọc tiếp
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình vuông cạnh a. Tính thể tích V của khối lăng trụ đã cho theo a, biết A'B = 2a.
A. V = 2 3 a 3
B. V = a3
C. V = 3 a 3
D. V = 3 a 3 3
cho hình lăng trụ ABCDA'B'C'D' đáy là hình thoi cạnh A tâm O, góc ABC=120°. góc giữa AA' và đáy là 60°. A' cách đều A,B,D. Tính thể tích ABCDA'B'C'D'
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại A,
B
A
C
^
120
o
và BC AA a
3
. Tính theo a thể tích V của khối lăng trụ ABC.ABC. A.
V
9
a
3
4...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, B A C ^ = 120 o và BC =AA' = a 3 . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = 9 a 3 4
B. V = 3 3 a 3 6
C. V = 3 3 a 3 2
D. V = 3 a 3 4