Đáp án C
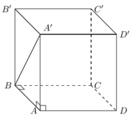
Diện tích đáy lăng trụ là a2.
Chiều cao của lăng trụ là A A ' = A ' B 2 - B A 2 = 4 a 2 - a 2 = a 3
Vậy thể tích lăng trụ là V = √3a3
Đáp án C

Diện tích đáy lăng trụ là a2.
Chiều cao của lăng trụ là A A ' = A ' B 2 - B A 2 = 4 a 2 - a 2 = a 3
Vậy thể tích lăng trụ là V = √3a3
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và A B C ⏜ = 120 0 Các cạnh AA, A'B, A'D cùng tạo với mặt đáy một góc bằng 60 0 . Tính theo a thể tích V của khối lăng trụ đã cho.
![]()
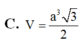
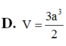
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi, biết A A ' = 4 a , A C = 2 a , B D = a . Thể tích V của khối lăng trụ là.
![]()
![]()
![]()
Lăng trụ tam giác ABC.A'B'C' có tam giác ABC vuông tại A; AB = a 3 ; BC = 2a. Biết AA' = A'B = A'C = a 3 . Tính thể tích V của hình lăng trụ.
A. V = a 3 2 3
B. V = a 3 6 3
C. V = a 3 6 2
D. V = a 3 2
Thể tích của khối lăng trụ đứng ABCD.A'B'C'D' có đáy là hình vuông cạnh a, A'B=2a.
A. V = a 3 3 3
B. V = a 3 3 6
C. V = a 3 3 2
D. V = a 3 3
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, B A C ^ = 120 o và BC =AA' = a 3 . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = 9 a 3 4
B. V = 3 3 a 3 6
C. V = 3 3 a 3 2
D. V = 3 a 3 4
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, mặt bên BCC'B' là hình vuông cạnh 2a. Tính thể tích V của khối lăng trụ ABC.A'B'C'.
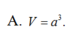
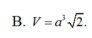
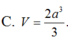
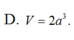
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông cân tại B, AB = a, A'B=a 3 . Thể tích khối lăng trụ ABC.A'B'C' bằng:
A. a 3 3 2
B. a 3 6
C. a 3 2
D. a 3 2 2
Cho lăng trụ tứ giác ABCD.A'B'C'D' có đáy là hình vuông cạnh a biết A'B' bằng a√2 tính thể tích lăng trụ