Đáp án B
Phương pháp : Chia cả tử và mẫu cho x và sử dụng giới hạn 
Cách giải : 

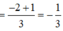
Đáp án B
Phương pháp : Chia cả tử và mẫu cho x và sử dụng giới hạn 
Cách giải : 

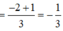
Giới hạn lim n → → + ∞ 1 + 2 + 3 + . . . + n - 1 + n n 2 bằng
A. + ∞
B. 1
C. 0
D. 1 2
Tính giới hạn lim x → − 2 − 3 + 2 x x + 2 .
A. - ∞
B. 2
C. + ∞
D. 3 2
Tính giới hạn lim x → 2 - 3 + 2 x x + 2
A. - ∞
B. 2
C. + ∞
D. 3 2
Tính giới hạn lim x → − 2 − 3 + 2 x x + 2 .
A. - ∞
B. 2.
C. + ∞
D. 3 2
Tính giới hạn lim x → 2 - 3 + 2 x x + 2 .
A. - ∞
B. 2
C. + ∞
D. 3 2
Cho a, b, c là các số thực khác 0. Để giới hạn lim x → − ∞ x 2 − 3 x + a x b x − 1 = 3 thì
A. a − 1 b = 3.
B. a + 1 b = 3.
C. − a − 1 b = 3.
D. a − 1 − b = 3.
Cho hàm số f(x) xác định và liên tục trên đoạn [-5;3] có đồ thị như hình vẽ bên. Biết diện tích các hình phẳng (A), (B), (C), (D) giới hạn bởi đồ thị hàm số f(x) và trục hoành lần lượt bẳng 6; 3; 12; 2. Tích phân ∫ - 3 1 2 f 2 x + 1 + 1 d x bằng
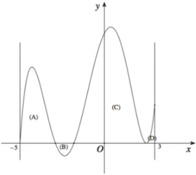
A. 27
B. 25
C. 17
D. 21
Tính diện tích S của hình phẳng (H) được giới hạn bởi các đồ thị d 1 : y = 2 x - 2 , d 2 : y = x 2 + 1 , P : y = x 2 - 4 x + 3
A. S = 189 16
B. S = 13 3
C. S = 487 48
D. S = 27 4
Cho hàm số f(n)= 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n . ( n + 1 ) . ( n + 2 ) = n ( n + 3 ) 4 ( n + 1 ) ( n + 2 ) ,n∈N*. Kết quả giới hạn l i m ( 2 n 2 + 1 - 1 ) f ( n ) 5 n + 1 = a b b ∈ Z . Giá trị của a 2 + b 2 là
A. 101
B. 443
C. 363
D. 402
Giới hạn l i m x → 3 x + 1 - 5 x + 1 x - 4 x - 3 bằng a b (phân số tối giản). Giá trị của a - b là:
A. 1
B. 1 9
C. -1
D. 9 8