HD: Phương trình tiếp tuyến là y = 4x - 3.
Phương trình hoành độ giao điểm
x2 +1 = 4x - 3 ⇔ x2 - 4x + 4 = 0 ⇔ x = 2.
Do đó diện tích phải tìm là:
Tính diện tích hình phẳng giới hạn bởi đường cong y = x 2 , tiếp tuyến với đường cong đó tại điểm có hoành độ bằng 2 và trục Oy.
A. − 40 3
B. 8 3
C. 20 3
D. 68 3
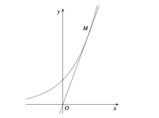
Cho hình phẳng (H) giới hạn bởi đường cong (C): y = e x , tiếp tuyến của (C) tại điểm M(1;e) và trục Oy. Diện tích của (H) bằng
A. (e+2)/2.
B. (e-1)/2.
C. (e+1)/2.
D. (e-2)/2.
Gọi diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 tiếp tuyến tại A(1;1) và trục Oy bằng S 1 . Diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 tiếp tuyến tại A(1;1) và trục Ox bằng S 2 . Khi đó, tỉ số S 1 S 2 bằng:
A. 1/4
B. 3
C. 1/3
D. 4
Gọi diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 , tiếp tuyến tại A(1;1) và trục Oy bằng S 1 . Diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 , tiếp tuyến tại A(1;1) và trục Ox bằng ( S 2 ) . Khi đó S 1 S 2 bằng
A. 1/4
B. 4
C. 1/3
D. 3
Gọi diện tích hình phẳng giới hạn bởi P : y = x 2 , tiếp tuyến tại A(1;1) và trục Oy bằng S 1 . Diện tích hình phẳng giới hạn bởi P : y = x 2 , tiếp tuyến tại A(1;1) và trục Ox bằng S 2 . Khi đó S 1 S 2 bằng
A. 1 4
B. 4
C. 1 3
D. 3
Diện tích S của hình phẳng giới hạn bởi parabol ( P ) : y = x 2 - 1 , tiếp tuyến của (P) tại M(0;1) và trục Oy là:
A. S = 1.
B . S = 1 4 .
C . S = 1 3 .
D . S = 7 3 .
Diện tích hình phẳng được giới hạn bởi đường cong y = x 2 và đường thẳng y = 2 x + 3 , trục hoành trong miền x ≥ 0 bằng
A. 12
B. 32 3
C. 9
D. 5 3
Diện tích hình phẳng được giới hạn bởi đường cong y = x 2 và đường thẳng y = 2 x + 3 , trục hoành trong miền x ≥ 0 bằng
A. 12
B. 9
C. 5 3
D. 32 3
Tính diện tích hình phẳng giới hạn bởi đường cong y = x 2 - x + 3 và đường thẳng y=2x+1
A. 1/3
B. 1/6
C. 1/4
D. 1/2
