a) \(x\left(x-6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
b) \(\left(-7-x\right)\left(-x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}-7-x=0\\-x+5=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-7\\x=-5\end{matrix}\right.\)
c) \(\left(x+3\right)\left(x-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+3=0\\x-7=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-3\\x=7\end{matrix}\right.\)
d) \(\left(x-3\right)\left(x^2+12\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\x^2+12=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x^2=-12\text{(vô lý)}\end{matrix}\right.\)
\(\Rightarrow x=3\)
e) \(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x+1\ge0\\2-x\ge0\end{matrix}\right.\\\left[{}\begin{matrix}x+1\le0\\2-x\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x\ge-1\\x\le2\end{matrix}\right.\\\left[{}\begin{matrix}x\le-1\\x\ge2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}-1\le x\le2\\x\in\varnothing\end{matrix}\right.\)
\(\Rightarrow-1\le x\le2\)
f) \(\left(x-3\right)\left(x-5\right)\le0\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x-3\le0\\x-5\ge0\end{matrix}\right.\\\left[{}\begin{matrix}x-3\ge0\\x-5\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\\\left[{}\begin{matrix}x\ge3\\x\le5\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow3\le x\le5\)
a) =>\(\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.=>\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
b => \(\left[{}\begin{matrix}-7-x=0\\-x+5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-7\\x=5\end{matrix}\right.\)
d) => \(\left[{}\begin{matrix}x-3=0\\x^2+12=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=3\\x^2=-12\end{matrix}\right.\)(vô lí) => x=3
c) => \(\left[{}\begin{matrix}x+3=0\\x-7=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-3\\x=7\end{matrix}\right.\)
a) x.(x - 6) = 0 \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
b) (-7 - x)(-x + 5) = 0
\(\Leftrightarrow\left[{}\begin{matrix}-7-x=0\\-x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-7\\x=5\end{matrix}\right.\)
c) (x + 3)(x - 7) = 0
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=7\end{matrix}\right.\)
d) (x - 3)(x2 + 12) = 0
Ta có: x2 ≥ 0 ∀ x => x2 + 12 ≥ 12 ∀ x ∈ Z
mà (x - 3)(x2 + 12) = 0 nên x - 3 = 0 \(\Leftrightarrow\)x = 3
e) (x + 1)(2 - x) ≥ 0
+) Xét: (x + 1)(2 - x) = 0 \(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\2-x=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
+) Xét: (x + 1)(2 - x) > 0
=> x + 1 và 2 - x cùng dấu
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+1>0\\2-x>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+1< 0\\2-x< 0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>-1\\x< 2\end{matrix}\right.\\\left\{{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}-1< x< 2\\2< x< -1\end{matrix}\right.\)
=> -1 < x < 2 ( do 2 < x < -1 là vô lí)
mà x ∈ Z nên x ∈ {0; 1}
f) (x - 3)(x - 5) = x(x - 5) - 3(x - 5)
= x2 - 5x - 3x + 15 = (x2 - 2.x.4 + 42) - 1
= (x - 1)2 - 1
Có: (x - 1)2 ≥ 0 ∀ x ∈ Z => (x - 1)2 - 1 ≥ -1
=> (x - 3)(x - 5) ≥ -1
mà (x - 3)(x - 5) ≤ 0 nên -1 ≤ (x - 3)(x - 5) ≤ 0
Mặt khác: (x - 3)(x - 5) ∈ Z (do x ∈ Z)
=> (x - 3)(x - 5) = -1 hoặc (x - 3)(x - 5) = 0
Xét: (x - 3)(x - 5) = -1
=> x - 3 và x - 5 trái dấu mà x ∈ Z
=> x - 3 = -1 ; x - 5 = 1 hoặc x - 3 = 1 ; x - 5 = -1
=> x = 2 ; x = 6 hoặc x = 4 ; x = 4
Xét: (x - 3)(x - 5) = 0 \(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=5\end{matrix}\right.\)












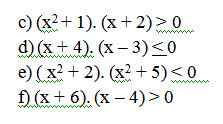 Giúp mình với, mình cần gấp ạ
Giúp mình với, mình cần gấp ạ





