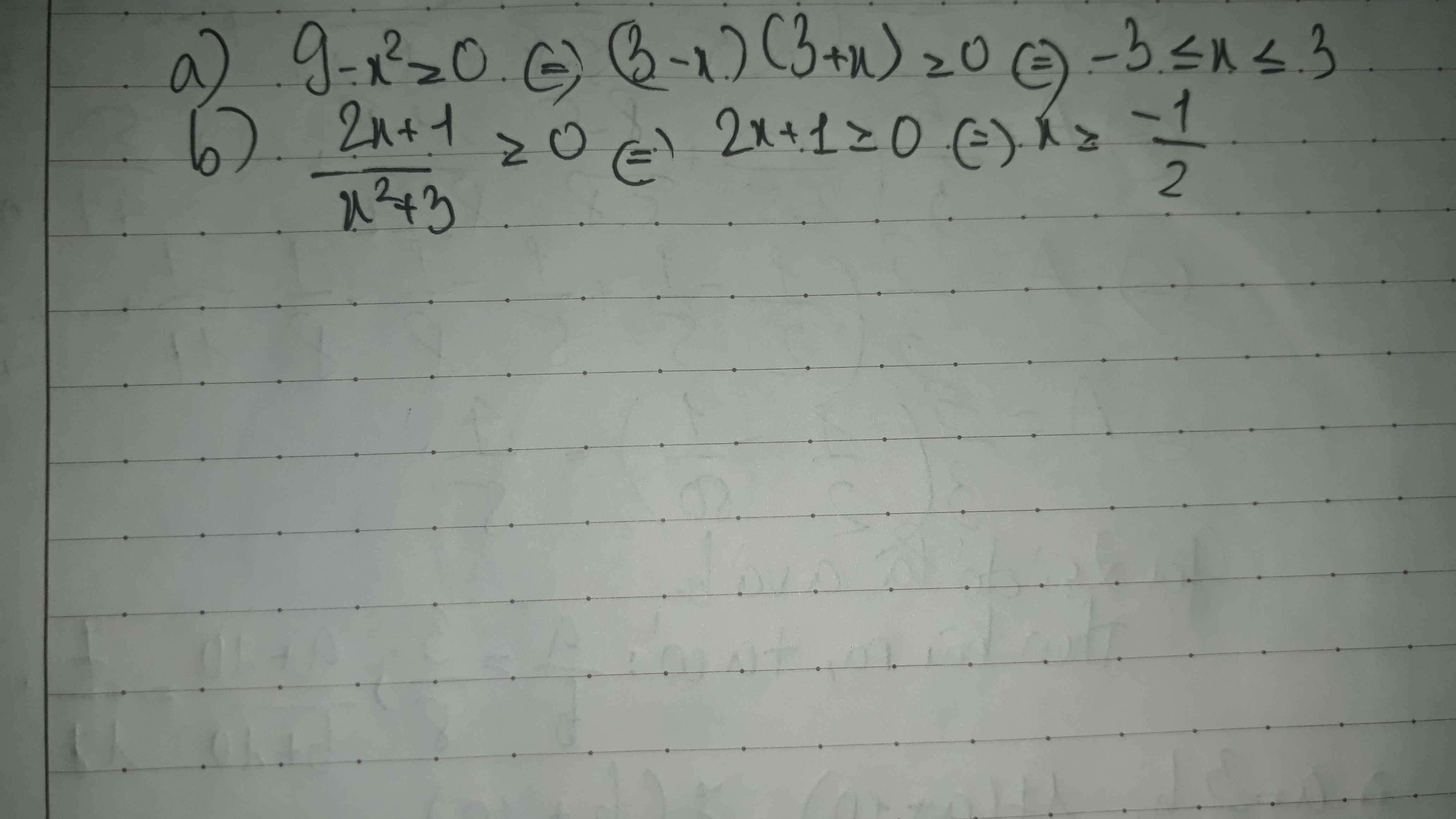Để\(\sqrt{9-x^2}\) dc xác định
Thì\(9-x^2\ge0\Leftrightarrow\left(3-x\right)\left(3+x\right)\ge0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3-x\ge0\\3+x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}3-x\le0\\3-x\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\le3\\x\ge-3\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow-3\le x\le3\)
Để\(\sqrt{\dfrac{2x+1}{x^2+3}}\)dc xác định
Thì\(\left\{{}\begin{matrix}2x+1\ge0\\x^2+3>0\left(HN\right)\end{matrix}\right.\)
\(\Leftrightarrow2x\ge-1\)
\(\Leftrightarrow x\ge\dfrac{-1}{2}\)
\(\)
a) Để \(\sqrt{9-x^2}\) xác định thì \(9-x^2\ge0\)
\(\Leftrightarrow x^2-9\le0\)
\(\Leftrightarrow-3\le x\le3\)
b) Để \(\sqrt{\dfrac{2x+1}{x^2+3}}\) xác định thì \(2x+1\ge0\)
hay \(x\ge-\dfrac{1}{2}\)