Đáp án D
Phương pháp giải:
Cô lập tham số m, đưa về khảo sát hàm số để biện luận số nghiệm của phương trình
Lời giải:
Xét hàm số ![]() có
có ![]()
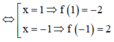
Để phương trình F(x) = m – 1 có 3 nghiệm phân biệt
![]()
Đáp án D
Phương pháp giải:
Cô lập tham số m, đưa về khảo sát hàm số để biện luận số nghiệm của phương trình
Lời giải:
Xét hàm số ![]() có
có ![]()
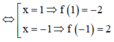
Để phương trình F(x) = m – 1 có 3 nghiệm phân biệt
![]()
Tất cả giá trị của m để phương trình m x - x - 3 = m + 1 có hai nghiệm thực phân biệt.
A. m >0.
B. 1 2 ≤ m ≤ 3 2
C. 1 2 ≤ m ≤ 1 + 3 4
D. 0 < m < 1 + 4
Tìm tất cả giá trị của m để phương trình x 4 - 2 ( m + 1 ) x 2 + m 2 - 3 = 0 có 4 nghiệm thực phân biệt?
A . ( 3 ; + ∞ )
B . [ 3 ; + ∞ )
C . ( 1 ; 6 )
D . [ 1 ; 6 )
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị như hình bên. Tất cả các giá trị của m để phương trình | f ( x ) | + m - 1 = 0 có 3 nghiệm phân biệt là
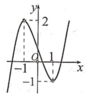
A. m=1
B. m=2
C. m = ± 1
D. m=0
Tìm tất cả các giá trị của m để phương trình log 2 3 x − 2 − log 2 3 x + 1 = m có 3 nghiệm phân biệt?
A.m > 3
B. m < 2
C. m > 0
D. m=0
Cho phương trình log 3 2 x − 4 log 3 x + m − 3 = 0 . Tìm tất cả các giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thỏa mãn x 1 > x 2 > 1
A. 6
B. 4
C. 3
D. 5
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình 9 1 - x + 2 ( m - 1 ) 3 1 - x + 1 = 0 có 2 nghiệm phân biệt.
A. m > 1
B. m < -1
C. m < 0
D. -1 < m < 0
Tìm tất cả các giá trị thực của m để phương trình 21 o g 2 | x | + l o g 2 | x + 3 | = m có đúng 3 nghiệm thực phân biệt.
A. m ∈ (0; 2)
B. m ∈ {0; 2}
C. m ∈ ( - ∞ ; 2 )
D. m ∈ {2}
Cho hàm số y = f(x) có bảng biến thiên như sau:
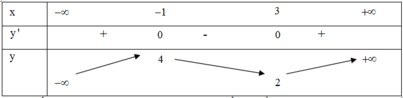
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m + 1 có 3 nghiệm thực phân biệt?
A. –3 ≤ m ≤ 3
B. –2 ≤ m ≤ 4
C. –2 < m < 4
D. –3 < m < 3
Tìm tất cả các giá trị của tham số thực m để phương trình sau có đúng 3 nghiệm thực phân biệt 9 x 2 - 2 . 3 x 2 + 1 + 3 m - 1 = 0
A. m = 10 3
B. 2 < m < 10 3
C. m = 2
D. m < 2