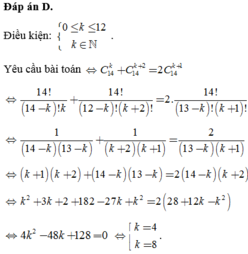Các câu hỏi tương tự
Có tất cả bao nhiêu bộ số nguyên dương (k,n) biết n20 và các số
C
n
k
-
1
;
C
n
k
;
C
n
k
+
1
theo thứ tự đó là số hạng thứ nhất, thứ ba, thứ năm của một cấp số cộng. A. 4 B. 2 C. 1 D. 0
Đọc tiếp
Có tất cả bao nhiêu bộ số nguyên dương (k,n) biết n<20 và các số C n k - 1 ; C n k ; C n k + 1 theo thứ tự đó là số hạng thứ nhất, thứ ba, thứ năm của một cấp số cộng.
A. 4
B. 2
C. 1
D. 0
Cho hàm số
y
x
3
-
3
x
2
+
4
có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là A. {0} B. R C. {-3} D. (-3; +∞).
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
A. {0}
B. R
C. {-3}
D. (-3; +∞).
Cho K là tập hợp các số tự nhiên có bốn chữ số. Chọn ngẫu nhiên một số từ K. Tính xác suất để số được chọn có tổng các chữ số là bội của 4 .
Cho khối lăng trụ đứng, mặt phẳng (P) đi qua C và các trung điểm của AA, BB chia khối lăng trụ ABC. ABC thành hai khối đa diện có tỷ số thể tích bằng k với k ≤ 1. Tìm k. A.
1
3
B.
2
3
C. 1 D.
1
2
Đọc tiếp
Cho khối lăng trụ đứng, mặt phẳng (P) đi qua C' và các trung điểm của AA', BB' chia khối lăng trụ ABC. A'B'C' thành hai khối đa diện có tỷ số thể tích bằng k với k ≤ 1. Tìm k.
A. 1 3
B. 2 3
C. 1
D. 1 2
Cho hàm số y x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y 0 là A. 1 B. 2 C. 3 D. không có giá trị nào của m thỏa mãn
Đọc tiếp
Cho hàm số y= x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y= 0 là
A. 1
B. 2
C. 3
D. không có giá trị nào của m thỏa mãn
Cho đồ thị C: y 2x3-3x2-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k để C cắt d tại ba điểm phân biệt là A.
k
9
8
k
≠
0
B.
k...
Đọc tiếp
Cho đồ thị C: y= 2x3-3x2-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k để C cắt d tại ba điểm phân biệt là
A. k < 9 8 k ≠ 0
B. k > - 9 8 k ≠ 0
C. k < - 9 8 k ≠ 0
D. k > 9 8 k ≠ 0
n là số nguyên dương và k là tích của tất cả các số nguyên từ 1 đến n. Nếu k là bội số của 1440 thì giá trị nhỏ nhất có thể có của n là A. 8 B. 12 C. 16 D. 18 E. 24
Cho hàm số:a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.b) Viết phương trình tiếp tuyến của (C) tại các giao điểm của nó với trục Ox.c) Biện luận theo k số giao điểm của (C) với đồ thị (P) của hàm số: y k – 2
x
2
.
Đọc tiếp
Cho hàm số:
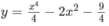
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của (C) tại các giao điểm của nó với trục Ox.
c) Biện luận theo k số giao điểm của (C) với đồ thị (P) của hàm số: y = k – 2 x 2 .
Cho hàm số y = x 3 - 3 x 2 + 2 x - 9 có đồ thị (C). Gọi k là hệ số góc của các tiếp tuyến của (C) thì giá trị nhỏ nhất của k là
A. Không tồn tại
B. 1
C. -1
D. 0