Chọn B
Điều kiện: ![]() ,
,
đặt ![]() .
.
Khi đó phương trình trở thành ![]() .
.
Tìm GTLN – GTNN của hàm ![]() .
.
Chọn B
Điều kiện: ![]() ,
,
đặt ![]() .
.
Khi đó phương trình trở thành ![]() .
.
Tìm GTLN – GTNN của hàm ![]() .
.
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 5 x - 1 . log 4 2 . 5 x - 2 = m có nghiệm x ≥ 1
A. m ∈ (-∞;2)
B. m ∈ (2;+∞)
C. m ∈ (3;+∞)
D. m ∈ (-∞;3)
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 2 5 x - 1 . log 2 2 . 5 x - 2 ≥ m có nghiệm x ≥ 1
A. m ≥ 6
B. m > 6
C. m ≤ 6
D. m < 6
Tìm tập hợp tất cả các giá trị của tham số m để phương trình 5 x + 2 - x - 5 m = 0 có nghiệm thực
![]()
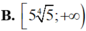
![]()
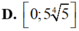
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0
với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ∈ ( - ∞ , 0 )
A. m > 2 + 2 3 3
B. m > 2 - 2 3 3
C. m ≥ 2 - 2 3 3
D. m ≥ - 2 - 2 3 3
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm: x + 5 + 4 - x ≥ m
A. 1
B. 2
C. 3
D. 4
Cho phương trình m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x1, x2 thỏa 0 < x1 < 1 < x2
A. 2 ; + ∞
B. - 1 ; 2
C. - ∞ ; - 1
D. - ∞ ; - 1 ∪ 2 ; + ∞
Tìm tất cả các giá trị thực của tham số m để bất phương trình log2( 5x - 1) .log2)( 2.5x - 2) > m - 1 có nghiệm x ≥ 1?
A. m ≥ 7
B. m > 7
C. m ≤ 7
D. m < 7
Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau có nghiệm x 2 + 4 x + y = m 2 x 2 + x y ( x + 2 ) = 9
A. m ≥ 6
B. - 10 ≤ m ≤ 6
C. m ≤ - 10
D. m ≤ - 10 hoặc m ≥ 6
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau.
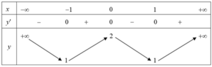
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) - m =0 có 4 nghiệm phân biệt.
A. m ∈ ( 1 ; 2 ]
B. m ∈ [ 1 ; 2 )
C. m ∈ ( 1 ; 2 )
D. m ∈ [ 1 ; 2 ]
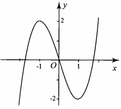
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình | x | 3 - 3 | x | = 2 m có 4 nghiệm phân biệt
A.![]()
B. ![]()
C.![]()
D. ![]()