Đáp án D
Từ đồ thị hàm số đã cho (như hình vẽ) ta suy ra đồ thị của hàm số
![]()
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán
: ![]()
Đáp án D

Từ đồ thị hàm số đã cho (như hình vẽ) ta suy ra đồ thị của hàm số
![]()
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán
: ![]()
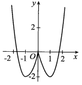
Cho hàm số y =f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + 1 = m có bốn nghiệm thực phân biệt?
![]()
![]()
![]()
![]()
Hình bên là đồ thị của hàm số y = 2 x + 1 x - 1 Tìm tất cả các giá trị thực của tham số m để phương trình 2 x + 1 | x - 1 | = m có hai nghiệm phân biệt.
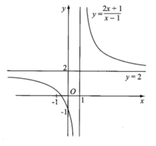
A. m > 2
B. Không có giá trị của m.
C. m > -2
D. Với mọi m.
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình 64 | x | 3 = ( x 2 + 1 ) 2 ( 12 | x | + m ( x 2 + 1 ) ) có nghiệm.
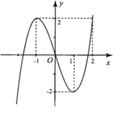
A.![]()
B. Với mọi m
C. ![]()
D. ![]()
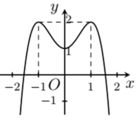
Cho hàm số y = f ( x ) liên tục trên R và có đồ thị hàm số đường cong trong hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình | f ( x ) | = m có 4 nghiệm phân biệt.
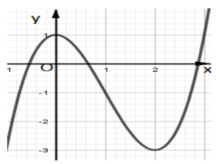
A. m ∈ (0;3)
B. -3 < m < 1
C. Không có giá trị nào của m.
D. 1 < m < 3
Hình bên là đồ thị hàm số y = 2 x + 1 x - 1 Tìm tất cả các giá trị thực của tham số m để phương trình | 2 x + 1 | | x - 1 | = 2 m có hai nghiệm phân biệt
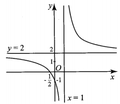
A.Với mọi m
B. Không có giá trị của m
C.![]()
D. ![]()
Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình
2 f ( x ) - m = 0 có đúng bốn nghiệm phân biệt.
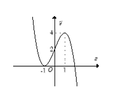
A. 0< m< 8
B.m> 4
C.m< 0 ; m> 8
D. -2< m< 4
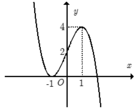
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị như hình bên. Tất cả các giá trị của m để phương trình f x + m - 1 = 0 có 3 nghiệm phân biệt là:

A. m=1.
B. m=2.
C. m= ± 1.
D. m=0.
Hình bên là đồ thị của hàm số y = 2 x 4 - 4 x 2 + 1 Tìm tất cả các giá trị thực của tham số m để phương trình 2 x 4 - 4 x 2 + 1 = 1 - m có 4 nghiệm phân biệt.
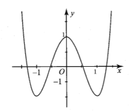
A. m = 0
B. m < 0
C. 0 < m < 1
D. m = 1
Cho hàm số y=f(x) có đồ thị như hình vẽ dưới đây. Gọi S là tập hợp tất cả các giá trị của tham số m để phương trình f ( 3 - 4 - x 2 ) = m có hai nghiệm phân biệt thuộc đoạn - 2 ; 3 . Tìm tập S.
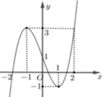
A. S = ( - 1 ; f 3 - 2 ]
B. S = ( f 3 - 2 ; 3 ]
C. S = ○
D. S = [-1;3]