
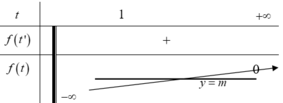
Dựa vào bảng biến thiên để phương trình có nghiệm -> m<0


Dựa vào bảng biến thiên để phương trình có nghiệm -> m<0
Tìm tất cả các giá trị thực của tham số m để bất phương trình ( m + 1 ) x 2 - 2 ( m + 1 ) x + 4 ≥ 0 ( 1 ) có tập nghiệm S = ℝ ?
A. m > - 1
B. - 1 ≤ m ≤ 3
C. - 1 < m ≤ 3
D. - 1 < m < 3
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình 9 1 - x + 2 ( m - 1 ) 3 1 - x + 1 = 0 có 2 nghiệm phân biệt.
A. m > 1
B. m < -1
C. m < 0
D. -1 < m < 0
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0 với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho có nghiệm đúng với mọi x ∈ - ∞ ; 0
A. m ≥ 2 - 2 3 3
B. m > 2 - 2 3 3
C. m > 2 + 2 3 3
D. m ≥ - 2 - 2 3 3
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 3 x + m - 1 3 x + m - 1 > 0 nghiệm đúng ∀ x ∈ ℝ .
A . m ∈ R
B . m > 1
C . m ≤ 1
D . m ≥ 1
Cho bất phương trình 9 x + ( m - 1 ) 3 x + m > 0 ( 1 ) . Tìm tất cả các giá trị của tham số m để bất phương trình (1) nghiệm đúng ∀ x > 1
A. m ≥ - 3 2
B. m > - 3 2
C. m > 3 + 2 2
D. m ≥ 3 + 2 2
Cho bất phương trình m .3 x + 1 + 3 m + 2 4 − 7 x + 4 + 7 x > 0 , với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ∈ − ∞ ; 0 .
A. m > 2 + 2 3 3 .
B. m > 2 − 2 3 3 .
C. m ≥ 2 − 2 3 3 .
D. m ≥ − 2 − 2 3 3 .
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 5 x - 1 . log 4 2 . 5 x - 2 = m có nghiệm x ≥1?
A. m ϵ [2;+∞).
B. m ϵ [3;+∞).
C. m ϵ (-∞;2].
D. m ϵ (-∞;3].
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 0 , 02 log 2 3 x + 1 > log 0 , 02 m có nghiệm với mọi x ∈ - ∞ ; 0
A. m > 9
B. m < 2
C. 0 < m < 1
D. m ≥ 1
Tìm tất cả các giá trị thực của tham số m để phương trình 3 2 x - 1 + 2 m 2 - m - 3 = 0 có nghiệm
A. m ∈ - 1 ; 3 2
B. m ∈ 1 2 ; + ∞
C. m ∈ 0 ; + ∞
D. m ∈ - 1 ; 3 2
Cho phương trình m + 1 log 2 2 x + 2 log 2 x + ( m - 2 ) = 0 . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x 1 , x 2 thỏa 0 < x 1 < 1 < x 2 .
A. 2 ; + ∞
B. - 1 ; 2
C. - ∞ ; - 1
D. - ∞ ; - 1 ∪ 2 ; + ∞