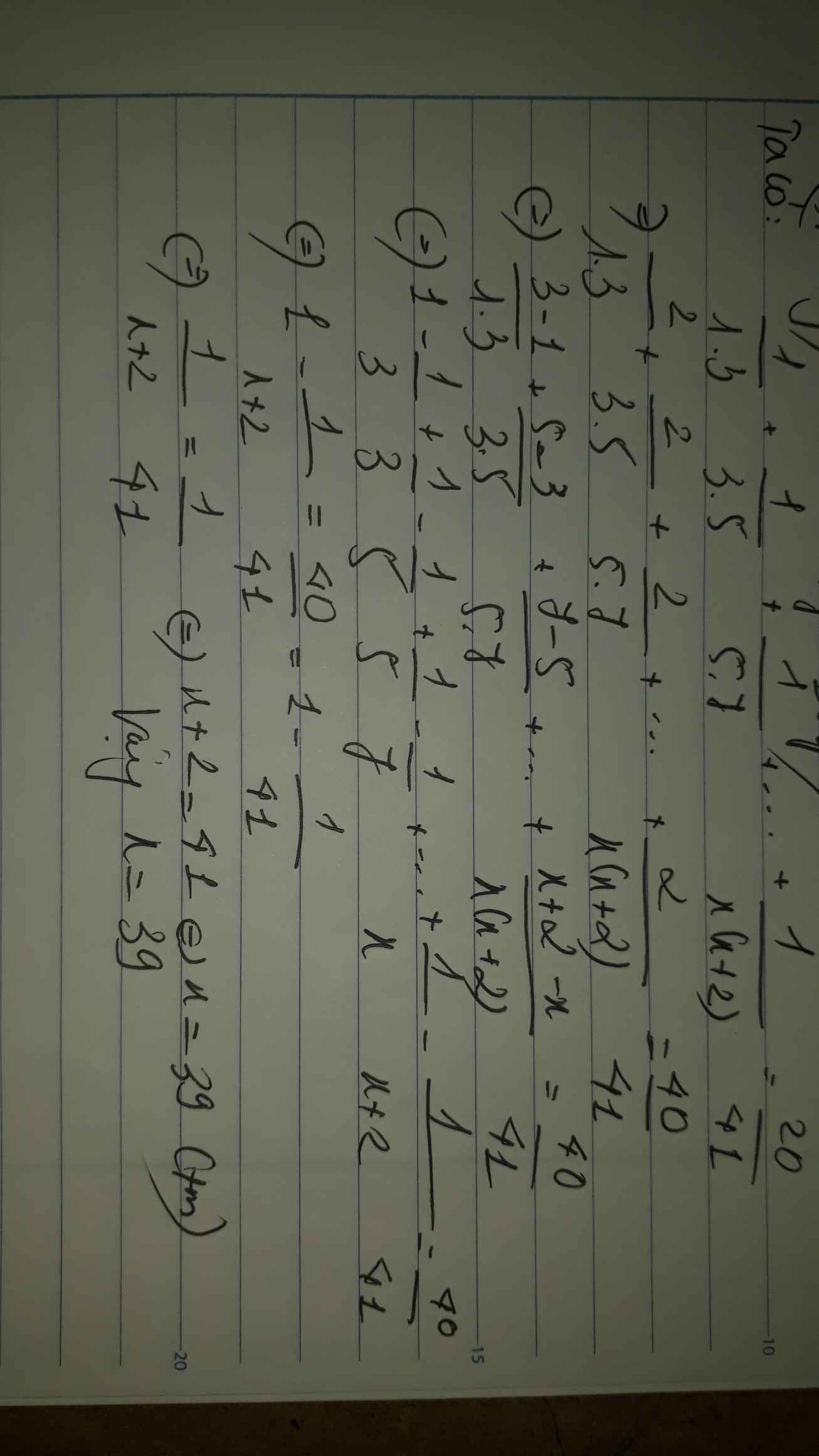Ta có: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{x\left(x+2\right)}=\dfrac{20}{41}\)
\(\Leftrightarrow\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{x\left(x+2\right)}=\dfrac{40}{41}\)
\(\Leftrightarrow1-\dfrac{2}{x+2}=\dfrac{40}{41}\)
\(\Leftrightarrow\dfrac{2}{x+2}=\dfrac{1}{41}\)
Suy ra: x+2=82
hay x=80
\(Tìm.x:\)
\(2x-\left(1+\dfrac{1}{1.3}\right).\left(1+\dfrac{1}{2.4}\right).\left(1+\dfrac{1}{3.5}\right)...\left(1+\dfrac{1}{2019+2021}\right)=x+1\)
ét o ét .-.
\(\dfrac{1}{1.3}\) +\(\dfrac{1}{3.5}\) +\(\dfrac{1}{5.7}\) +.....+\(\dfrac{1}{2003.2005}\)
Tính
\(\dfrac{1}{1.3}\)+ \(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+...+\(\dfrac{1}{2021.2023}\)
tính
\(B=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\)
Tính nhanh:
\(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2021.2023}\)
\(\dfrac{1}{1.3}\) + \(\dfrac{1}{3.5}\) + \(\dfrac{1}{5.7}\) +......+ \(\dfrac{1}{(2x-1)(2x+1)}\) = \(\dfrac{49}{99}\)
HeLp me
tiếp help A=\(\dfrac{1}{1.3}\)+\(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+.....+\(\dfrac{1}{99.101}\) help me :)
tính tổng có quy luật :
H=\(\dfrac{1}{1.3}\)+\(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+......+\(\dfrac{1}{47.49}\)+\(\dfrac{1}{49.51}\)
Thực hiện phép tính:
\(\left(1+\dfrac{1}{1.3}\right)+\left(1+\dfrac{1}{2.4}\right)+\left(1+\dfrac{1}{3.5}\right)+...+\left(1+\dfrac{1}{2019.2021}\right)\)
