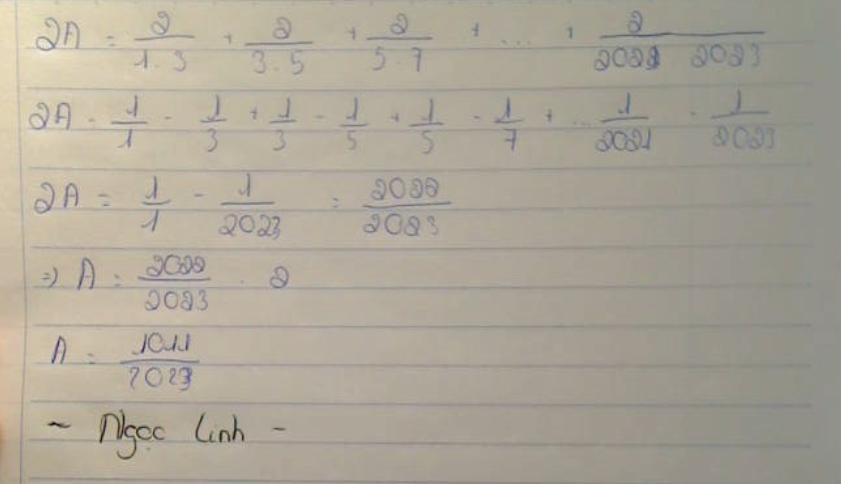Question

Tính nhanh:

\(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2021.2023}\)

Answer 1

chữ xấu (thông cảm) ;-;

Answer 2

\(A=1.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{5}+...+\dfrac{1}{2021}.\dfrac{1}{2023}=1-\dfrac{1}{2023}=\dfrac{2022}{2023}\)

Answer 3

\(A=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2021\cdot2023}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)

\(=\dfrac{1}{2}\cdot\dfrac{2022}{2023}=\dfrac{1011}{2023}\)

Answer 4

`A=1/[1.3]+1/[3.5]+1/[5.7]+....+1/[2021.2023]`

`A=1/2.(2/[1.3]+2/[3.5]+2/[5.7]+....+2/[2021.2023])`

`A=1/2.(1-1/3+1/3-1/5+1/5-1/7+.....+1/2021-1/2023)`

`A=1/2.(1-1/2023)`

`A=1/2 . 2022/2023`

`A=1011/2023`

Answer 5

Answer 6