Chọn A.
Phương pháp:
Áp dụng công thức khai triển nhị thức Newton:
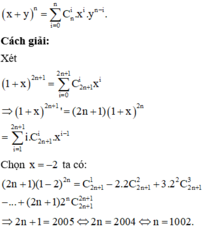
Chọn A.
Phương pháp:
Áp dụng công thức khai triển nhị thức Newton:
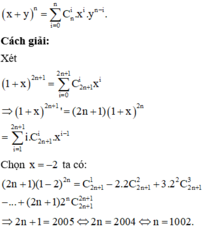
Bài 11:a,Tìm các số nguyên x sao cho (4x-3) chia hết cho (x-2) b,Tìm n biết 5n+7 chia hết cho 3n+2 c,Tìm n thuộc Z,biết 3n+2 chia hết cho n-1
Tìm số nguyên n sao cho :
a)3n+2 chia hết cho n-1
b)3n+24 chia hết cho n-4
c)3n+5 chia hết cho n+1
Biết rằng 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n ( n + 1 ) ( n + 2 ) = a n 2 + b n c n 2 + d n + 16 trong đó a,b,c,d và n là các số nguyên dương.Tính giá trị của biểu thức T=a+b+c+d
A. 45
B.40
C. 38
D. 24
Tìm số nguyên dương n nhỏ nhất sao n^2+5n+1 cho là số nguyên tố. Trả lời: n=.........
Cho dãy số u n được xác định bởi u 1 = 2 ; u n = 2 u n - 1 + 3 n - 1 . Công thức số hạng tổng quát của dãy số đã cho là biểu thức có dạng a . 2 n b n + c , với a, b, c là các số nguyên, n ≥ 2 , n ∈ N . Khi đó, tổng a + b + c có giá trị bằng ?
A. -4
B. 4
C. -3
D. 3
Tìm n\(\in\)Z, sao cho:
a) \(\frac{n+3}{n-2}\) là số nguyên âm
b) \(\frac{n+7}{3n-1}\) là số nguyên
c) \(\frac{3n+2}{4n-5}\) là số tự nhiên
Cho dãy số ( a n ) thỏa mãn a 1 = 1 và 5 a n + 1 - a n - 1 = 3 3 n + 2 , với mọi n ≥ 1 . Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 49
B. n = 41
C. n = 123
D. n = 39
Cho dãy số a n thỏa mãn a 1 = 1 và 5 a n + 1 - a n - 1 = 3 3 n + 2 với mọi n ≥ 1 Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 49
B. n = 41
C. n = 123
D. n = 39
Tìm số nguyên dương n sao cho
C 2 n + 1 1 - 2 . 2 . C 2 n + 1 2 + 3 . 2 . C 2 n + 1 3 - 4 . 2 3 . C 2 n + 1 4 + . . + 2 n + 1 2 2 n C 2 n + 1 2 n + 1 = 2019
A. 1009
B. 1010
C. 1011
D. 1012
Cho cấp số cộng (an), cấp số nhân (bn) thỏa mãn a2>a1≥0, b2>b1≥1 và hàm số f(x) = x3 – 3x sao cho f(a2) + 2 = f(a1) và f(log2b2) + 2 = f(log2b1). Tìm số nguyên dương n (n>1) nhỏ nhất sao cho bn > 2018an
A. 20
B. 10
C. 14
D. 16