Chọn B
Ta có 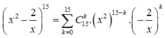
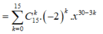
Số hạng không chứa x tương ứng với 30 - 3k = 0 => k = 10
Khi đó số hạng cần tìm là 2 10 . C 15 10 .
Chọn B
Ta có 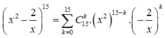
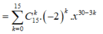
Số hạng không chứa x tương ứng với 30 - 3k = 0 => k = 10
Khi đó số hạng cần tìm là 2 10 . C 15 10 .
Tìm hệ số của số hạng chứa x^10 trong khai triển: (x^2-x^3+1)^10
Cho biểu thức: P(x) = ( 1 + x ) 9 + ( 1 + x ) 10 + ( 1 + x ) 11 + ( 1 + x ) 12 + ( 1 + x ) 13 + ( 1 + x ) 14 + ( 1 + x ) 15 . Hệ số của số hạng chứa x 9 trong khai triển thành đa thức của P(x) là
A. 3003
B. 8000
C. 8008
D. 3000
1/ Giải phương trình sau:
\(tan^2\left(x+\dfrac{\pi}{3}\right)+\left(\sqrt{3}-1\right)tan\left(x+\dfrac{\pi}{3}\right)-\sqrt{3}=0\)
2/ Tìm hệ số của số hạng chứa \(x^{26}\) trong khai triển \(\left(\dfrac{1}{x^4}+x^7\right)^n\) . Biết \(C^2_{n+2}-4C^n_{n+1}=2\left(n+1\right)\) (n ∈ N* ; x > 0)
Tìm hệ số của số hạng chứa \(x^5\) trong khai triển của đa thức: \(\left(x+2\right)^7\)
Tìm số hạng chứa x8 trong khai triển của biểu thức (x2-x)7
Tính giá trị của các bt sau(ko dùng máy tính) b/ B = 3cos 10 ° - 4cos^3 (10 °) . c/C = sin 30 ° * (2 - 4cos^2 15 °) d / D = 4sin^3 (40 °) + 3cos 130 °
tính giới hạn
a) \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{2x+10}-4}{3x-9}\)
b) \(\lim\limits_{x\rightarrow7}\dfrac{\sqrt{4x+8}-6}{x^2-9x+14}\)
c) \(\lim\limits_{x\rightarrow5}\dfrac{x^2-8x+15}{2x^2-9x-5}\)
Tìm số hạng chứa x5 trong khai triển \(\left(x-\dfrac{2}{x}\right)^{n^{ }}\) , biết n là số tự nhiên thỏa mãn \(C^3_n=\dfrac{4}{3}n+2C^2_n\)
A.144 B.134 C.115 D.141
Tìm số nguyên dương bé nhất n sao cho trong khai triển (x +1)n có hai hệ số liên tiếp có tỉ số là 7/15.
A. 20
B. 21
C. 22
D. 23
Tìm n ∈ N biết khai triển nhị thức ( a + 2 ) n + 4 , a ≠ 2 có tất cả 15 số hạng.
A. 13
B. 10
C. 17
D. 11