Chọn C
Ta có: 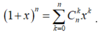 .
.
Số hạng tổng quát của khai triển là: ![]() . Hệ số của
x
k
trong khai triển là:
C
n
k
. Hệ số của
x
k
trong khai triển là:
C
n
k
Hệ số của số hạng chứa x 9 trong biểu thức P(x) là:
![]() .
.







