Chọn C.
Với x > 2 ta có hàm số liên tục
Để hàm số liên tục trên R thì hàm số phải liên tục trên khoảng (-∞; 2) và liên tục tại x = 2.
- Hàm số liên tục trên (-∞; 2) khi và chỉ khi tam thức
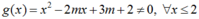
TH 1: 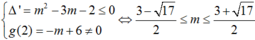
TH 2: 

Nên 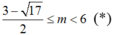 thì
thì ![]()
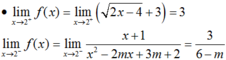
Hàm số liên tục tại  (thỏa (*))
(thỏa (*))
Chọn C.
Với x > 2 ta có hàm số liên tục
Để hàm số liên tục trên R thì hàm số phải liên tục trên khoảng (-∞; 2) và liên tục tại x = 2.
- Hàm số liên tục trên (-∞; 2) khi và chỉ khi tam thức
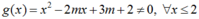
TH 1: 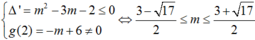
TH 2: 

Nên 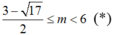 thì
thì ![]()
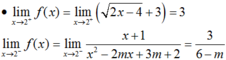
Hàm số liên tục tại  (thỏa (*))
(thỏa (*))
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ± 2
B. k ≠ 2
C. k ≠ - 2
D. k ≠ ± 1
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 x = 1 . Tìm k để f(x) gián đoạn tại x= 1.
A. K ≢ ± 2
B. K ≢ 2
C. K ≢ - 2
D. K ≢ ± 1
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ±2.
B. k ≠ 2.
C. k ≠ -2.
D. k ≠ ±1.
Cho hàm số f ( x ) = 4 - x 2 - 2 ≤ x ≤ 2 1 x > 2 . Tìm khẳng định đúng trong các khẳng định sau:
(I) f(x) không xác định tại x = 3
(II) f(x) liên tục tại x = -2
(III) lim x → 2 f ( x ) = 2
A. Chỉ (I).
B. Chỉ (I) và (II).
C. Chỉ (I) và (III).
D. Cả (I); (II); (III) đều sai.
Tìm a để các hàm số f ( x ) 3 x + 1 - 2 x 2 - 1 K h i x > 1 a ( x 2 - 2 ) x - 3 K h i x ≤ 1 liên tục tại x = 1
A. 1/2
B. 1/4
C. 3/4
D. 1
Cho hàm số f x = x + 1 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ± 2
B. k ≠ 2
C. k ≠ - 2
D. k ≠ ± 1
Cho hàm số f x = x + 1 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x= 1.
A. k ≠ ± 2
B. k ≠ 2
C. k ≠ - 2
D. k ≠ ± 1
cho hàm số f(x)=\(x^2-4x+3\)
tìm gtri tham số m để \(\left|f\left(\left|x\right|\right)-1\right|=m\) có 8 nghiệm phân biệt
đáp án:
A. \(m< 1\)
B.\(0\le x\le2\)
C.1<x<2
D.0<x<1
F(x) = \(\left\{{}\begin{matrix}\dfrac{x^3-x^2+2x-2}{x-1}\left(x\ne1\right)\\3x+m\left(x=1\right)\end{matrix}\right.\)
Tại x0=1. Tìm m để hàm số liên tục tại x0=1