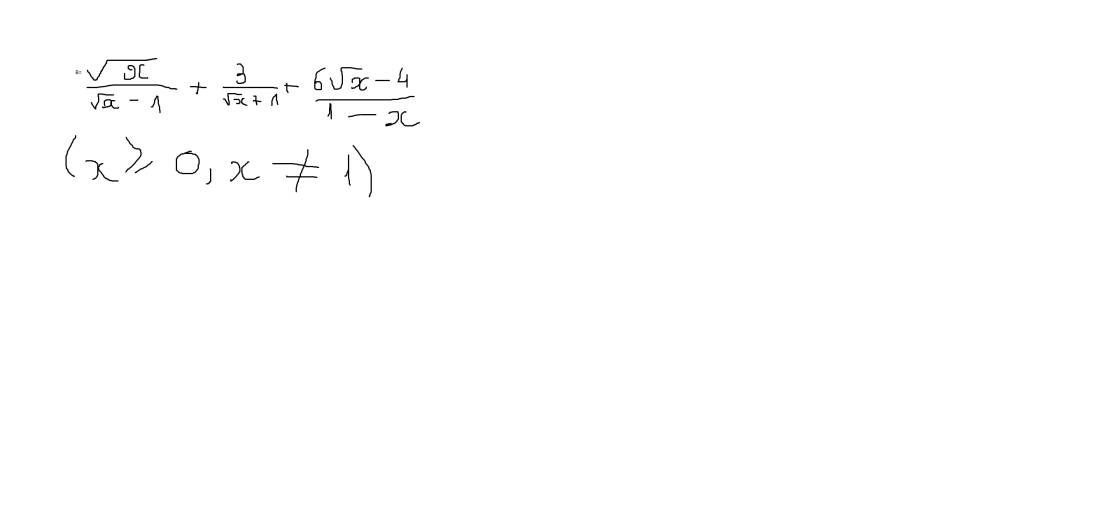\(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}+\dfrac{6\sqrt{x}-4}{1-x}\) \(\left(x\ge0;x\ne1\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{6\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
Mà: \(\left\{{}\begin{matrix}\sqrt{x}-1\ge-1\forall x\left(xđ\right)\\\sqrt{x}+1\ge1\forall x\left(xđ\right)\end{matrix}\right.\)
Nên: \(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\ge\dfrac{-1}{1}=-1\)
Dấu "=" xảy ra khi:
\(x=0\)
Vậy: GTNN của bt là -1 khi x=0
\(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}+\dfrac{6\sqrt{x}-4}{1-x}\) (ĐKXĐ: x ≥ 0; x ≠ 1)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{6\sqrt{x}-4}{x-1}\)
\(=\dfrac{x+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{3\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{6\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
Ta thấy: \(\left\{{}\begin{matrix}\sqrt{x}-1\ge-1\forall x\\\sqrt{x}+1\ge1\forall x\end{matrix}\right.\)
\(\Rightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\ge\dfrac{-1}{1}=-1\)
Dấu \("="\) xảy ra \(\Leftrightarrow\sqrt{x}=0\Leftrightarrow x=0\)
\(Vậy:GTNN\) của biểu thức là \(-1\) khi \(x=0\)
#\(Toru\)