Đáp án D.
Đây là hàm phân thức nên nó sẽ đơn điệu, do đó trên một khoảng nó sẽ đạt được min, max tại 2 đầu mút.
Có: y 0 = 1 3 ; y 2 = − 5 ⇒ min x ∈ 0 ; 2 y = − 5 ; max x ∈ 0 ; 2 y = 1 3
Đáp án D.
Đây là hàm phân thức nên nó sẽ đơn điệu, do đó trên một khoảng nó sẽ đạt được min, max tại 2 đầu mút.
Có: y 0 = 1 3 ; y 2 = − 5 ⇒ min x ∈ 0 ; 2 y = − 5 ; max x ∈ 0 ; 2 y = 1 3
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3 . Dưới đây là lời giải của học sinh:
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Tính y 0 = 3 ; y − 1 = y 1 = 1 . Vậy giá trị lớn nhất của hàm số là 3, và giá trị nhỏ nhất là 1.
Lời giải trên đúng hay sai? Nếu sai thì giải sai từ bước mấy?
A. Bước 2
B. Lời giải đúng
C. Bước 3
D. Bước 1
Cho bài toán : Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3
Dưới đây là lời giải của một học sinh.
Bước 1: Tập xác định D = ℝ . y ' = 8 x 3 − 8 x
Bước 2. Cho y' = 0 tìm x = 0 ; x = − 1 ; x = 1
Bước 3. Tính được y 0 = 3 ; y − 1 = 1 ; y 1 = 1. Vậy giá trị lớn nhất của hàm số là 3 , và giá trị nhỏ nhất là 1. Lời giải trên đúng hay sai? Nếu sai thì lời giải sai từ bước mấy?
A. Bước 2.
B. Lời giải đúng.
C. Bước 3.
D. Bước 1.
Tìm giá trị lớn nhất của hàm số y = x + 1 + 3 - x trên đoạn - 1 ; 3 .
A. m a x f x [ - 1 ; 3 ] = 2 3
B. m a x f x [ - 1 ; 3 ] = 3 2
C. m a x f x [ - 1 ; 3 ] = 2 2
D. m a x f x [ - 1 ; 3 ] = 2
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau

Biết rằng f(0)+f(3)=f(2)+f(5) Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) trên đoạn [0;5] lần lượt là
A. f(0), f(5)
B. f(2), f(0)
C. f(1), f(5)
D. f(2), f(5)
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Cho hàm số f x liên tục, không âm trên đoạn 0 ; π 2 thỏa mãn f 0 = 3 và f x . f ' x = cos x . 1 + f 2 x , ∀ x ∈ 0 ; π 2 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số f x trên đoạn π 6 ; π 2
A. m = 21 2 , M = 2 2
B. m = 5 2 , M = 3
C. m = 5 2 , M = 3
D. m = 3 , M = 2 2
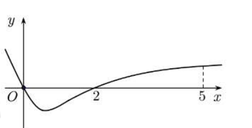
Cho hàm số f(x) có đạo hàm trên R và có đồ thị hàm y = f'(x) như hình vẽ. Biết rằng f ( 0 ) + f ( 3 ) = f ( 2 ) + f ( 5 ) . Giá trị nhỏ nhất và giá trị lớn của f(x) trên đoạn [0;5] lần lượt là:
A . f ( 2 ) ; f ( 0 )
B . f ( 0 ) ; f ( 5 )
C . f ( 2 ) ; f ( 5 )
D . f ( 1 ) ; f ( 3 )
Cho các mệnh đề :
1) Hàm số y=f(x) có đạo hàm tại điểm x 0 thì nó liến tục tại x 0 .
2) Hàm số y=f(x) liên tục tại x 0 thì nó có đạo hàm tại điểm x 0 .
3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).
4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Số mệnh đề đúng là:
A. 2
B. 4
C. 3
D. 1
Gọi (C) là đồ thị hàm số y = x - 7 x + 1 , A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0 < x M < 3 , tìm giá trị lớn nhất của diện tích ∆ A B M
A. 3
B. 5
C. 6
D. 3 5
Gọi (C) là đồ thị hàm số y = x - 7 x + 1 , A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0<xM<3, tìm giá trị lớn nhất của diện tích ∆ A M B
A. 3
B. 5
C. 5
D. 3 5