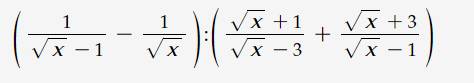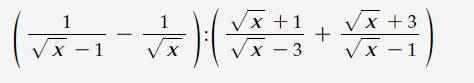\(\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\right)\) (ĐK: \(x>0;x\ne1;x\ne9\))
\(=\left[\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left[\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}+\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\right]\)
\(=\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1+x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{2x-10}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}{2\left(x-5\right)}\)
\(=\dfrac{\sqrt{x}-3}{2\sqrt{x}\left(x-5\right)}\)
\(=\dfrac{\sqrt{x}-3}{2x\sqrt{x}-10\sqrt{x}}\)
\(A>0\) khi
\(\dfrac{\sqrt{x}-3}{2x\sqrt{x}-10\sqrt{x}}>0\)
TH1:
\(\sqrt{x}-3>0\) và \(2x\sqrt{x}-10\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}>3\) và \(2\sqrt{x}\left(x-5\right)>0\)
\(\Leftrightarrow x>9\) và \(x>5\)
\(\Leftrightarrow x>9\)
TH2:
\(\sqrt{x}-3< 0\) và \(2x\sqrt{x}-10\sqrt{x}< 0\)
\(\Leftrightarrow\sqrt{x}< 3\) và \(2\sqrt{x}\left(x-5\right)< 0\)
\(\Leftrightarrow x< 9\) và \(x< 5\)
\(\Leftrightarrow x< 5\)
Vậy A > 0 khi \(\left[{}\begin{matrix}x>9\\x< 5\end{matrix}\right.\)
Ta có:
\(x=3-2\sqrt{2}=\left(\sqrt{2}\right)^2-2\cdot\sqrt{2}\cdot1+1^2=\left(\sqrt{2}-1\right)^2\)
\(A=\dfrac{\sqrt{\left(\sqrt{2}-1\right)^2}-3}{2\cdot\left(\sqrt{2}-1\right)^2\cdot\sqrt{\left(\sqrt{2}-1\right)^2}-10\cdot\sqrt{\left(\sqrt{2}-1\right)^2}}\)
\(A=\dfrac{\left|\sqrt{2}-1\right|-3}{2\cdot\left(3-2\sqrt{2}\right)\cdot\left|\sqrt{2}-1\right|-10\cdot\left|\sqrt{2}-1\right|}\)
\(A=\dfrac{\sqrt{2}-1-3}{\left(6-4\sqrt{2}\right)\left(\sqrt{2}-1\right)-10\left(\sqrt{2}-1\right)}\)
\(A=\dfrac{\sqrt{2}-4}{6\sqrt{2}-6-8+4\sqrt{2}-10\sqrt{2}+10}\)
\(A=\dfrac{\sqrt{2}-4}{-4}\)
\(A=\dfrac{4-\sqrt{2}}{4}\)