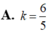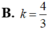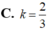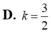Các câu hỏi tương tự
Cho hàm số y f(x)
a
x
+
b
c
x
+
d
( a,b,c,d
∈
ℝ
,
-
d
c
≠
0) đồ thị hàm số y f’(x) như hình vẽ. Biết đồ thị hàm số y f(x) cắt...
Đọc tiếp
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Cho hàm số y
x
3
-
3
(
m
+
3
)
x
2
+
3
có đồ thị (C). Tìm tất cả các giá trị của m sao cho qua điểm A(-1;1) kẻ được đúng 2 tiếp tuyến đến (C), Một tiếp tuyến là
△
1
:
y
-
1
và tiếp tuyến thứ 2 là thoả mãn tiếp xúc với (C) tại N đồng...
Đọc tiếp
Cho hàm số y = x 3 - 3 ( m + 3 ) x 2 + 3 có đồ thị (C). Tìm tất cả các giá trị của m sao cho qua điểm A(-1;1) kẻ được đúng 2 tiếp tuyến đến (C), Một tiếp tuyến là △ 1 : y = - 1 và tiếp tuyến thứ 2 là thoả mãn tiếp xúc với (C) tại N đồng thời cắt (C) tại P (khác N) có hoành độ bằng 3.
A. Không tồn tại m thoả mãn
![]()
![]()
![]()
Cho hàm số
y
x
3
-
3
(
m
+
3
)
x
2
+
3
có đồ thị (C). Tìm tất cả các giá trị của m sao cho qua điểm A(-1;1) kẻ được đúng 2 tiếp tuyến đến (C), Một tiếp tuyến là
∆
1
:
y
-
1
và tiếp tuyến thứ 2 là thoả mãn tiếp xúc với (C) tại N đồng thờ...
Đọc tiếp
Cho hàm số y = x 3 - 3 ( m + 3 ) x 2 + 3 có đồ thị (C). Tìm tất cả các giá trị của m sao cho qua điểm A(-1;1) kẻ được đúng 2 tiếp tuyến đến (C), Một tiếp tuyến là ∆ 1 : y = - 1 và tiếp tuyến thứ 2 là thoả mãn tiếp xúc với (C) tại N đồng thời cắt (C) tại P (khác N) có hoành độ bằng 3.
A. Không tồn tại m thoả mãn
B. m=2
C.m=0; m= -2
D. m= -2
Cho hàm số
y
x
+
2
2
x
+
3
có đồ thị (C). Giả sử, đường thẳng d: ykx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác
∆
O
A
B
cân tại gốc tọa độ O. Tổng k+m có giá trị bằng: A. 1. B. 3. C. -1. D. -3.
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác ∆ O A B cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1.
D. -3.
Cho hàm số
y
x
-
1
2
x
+
1
có đồ thị là (C). Gọi điểm M(x0; y0) với x0 -1 là điểm thuộc (C) biết tiếp tuyến của (C) tại điểm M cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB có trọng tâm G nằm trên đường t...
Đọc tiếp
Cho hàm số y = x - 1 2 x + 1 có đồ thị là (C). Gọi điểm M(x0; y0) với x0 > -1 là điểm thuộc (C) biết tiếp tuyến của (C) tại điểm M cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB có trọng tâm G nằm trên đường thẳng d: 4x+y=0. Hỏi giá trị của x0+2y0 bằng bao nhiêu?
A . -7/2
B. 7/2
C. 2
D.1
Cho hàm số y x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y 0 là A. 1 B. 2 C. 3 D. không có giá trị nào của m thỏa mãn
Đọc tiếp
Cho hàm số y= x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y= 0 là
A. 1
B. 2
C. 3
D. không có giá trị nào của m thỏa mãn
Cho hàm số
y
-
x
+
2
x
-
1
có đồ thị (C) và điểm A( a; 1). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến từ C đi qua A. Hỏi trong tập S có bao nhiêu giá trị nguyên A. 1. B. 0. C. 3. D. 4
Đọc tiếp
Cho hàm số y = - x + 2 x - 1 có đồ thị (C) và điểm A( a; 1). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến từ C đi qua A. Hỏi trong tập S có bao nhiêu giá trị nguyên
A. 1.
B. 0.
C. 3.
D. 4
Gọi D là hình phẳng giới hạn bởi đồ thị (C) của hàm số
y
x
4
-
2
x
2
+
1
tiếp tuyến D của (C) tại điểm có hoành độ x 2 và trục hoành. Quay D xung quanh trục hoành tạo thành một khối tròn xoay có thể tích V được tính theo công thức
Đọc tiếp
Gọi D là hình phẳng giới hạn bởi đồ thị (C) của hàm số y = x 4 - 2 x 2 + 1 tiếp tuyến D của (C) tại điểm có hoành độ x = 2 và trục hoành. Quay D xung quanh trục hoành tạo thành một khối tròn xoay có thể tích V được tính theo công thức
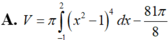
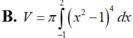
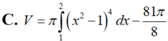
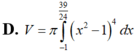
Diện tích hình phẳng giới hạn bởi đường cong
y
a
x
(a0), trục hoành và đường thẳng xa bằng
k
a
2
,
(
k
∈
ℝ
)
. Tính giá trị của tham số k.
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đường cong y = a x (a>0), trục hoành và đường thẳng x=a bằng k a 2 , ( k ∈ ℝ ) . Tính giá trị của tham số k.