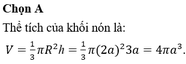Các câu hỏi tương tự
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Cho hình nón có thể tích bằng 12
π
và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương. A. 4 B. 3. C. 6 D. 5
Đọc tiếp
Cho hình nón có thể tích bằng 12 π và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương.
A. 4
B. 3.
C. 6
D. 5
Một khối trụ có thể tích bằng 25
π
. Nếu chiều cao khối trụ tăng lên năm lần và giữ nguyên bán kính đáy thì khối trụ mới có diện tích xung quanh bằng 25. Bán kính đáy của khối trụ ban đầu là: A.
r
10
B.
r
5
C.
r
2
D.
r
15
Đọc tiếp
Một khối trụ có thể tích bằng 25 π . Nếu chiều cao khối trụ tăng lên năm lần và giữ nguyên bán kính đáy thì khối trụ mới có diện tích xung quanh bằng 25. Bán kính đáy của khối trụ ban đầu là:
A. r = 10
B. r = 5
C. r = 2
D. r = 15
Hình nón tròn xoay có chiều cao
h
3
a
,
bán kính đường tròn đáy
r
a
.
Thể tích khối nón bằng A.
3
π
a
3
B.
π
a
3
9
C.
π
a
3
D.
π...
Đọc tiếp
Hình nón tròn xoay có chiều cao h = 3 a , bán kính đường tròn đáy r = a . Thể tích khối nón bằng
A. 3 π a 3
B. π a 3 9
C. π a 3
D. π a 3 3
Thể tích khối nón có bán kính bằng 2a và chiều cao bằng 3a là:
A. 2 πa 3
B. 4 πa 3
C. 12 πa 3
D. πa 3
Cho hai điểm A, B thuộc đồ thị hàm số y sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD 2 π /3. Độ dài của cạnh BC bằng A.
2
2
B.
1
2
C. 1 D.
3
2
Đọc tiếp
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
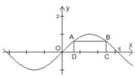
A. 2 2
B. 1 2
C. 1
D. 3 2
Một cái trống trường có bán kính hai đáy đều bằng 25 cm, thiết diện vuông góc với trục và cách đều hai đáy có chu vi 70
π
(cm). Chiều cao của trống bằng 80 cm. Biết rằng mặt phẳng chứa trục cắt mặt xung quanh của trống là các parabol (như hình vẽ). Hỏi thể tích của trống? A. 254259,6
c
m
3
B. 127129,8
c
m
3
C. 80933,3
c
m...
Đọc tiếp
Một cái trống trường có bán kính hai đáy đều bằng 25 cm, thiết diện vuông góc với trục và cách đều hai đáy có chu vi 70 π (cm). Chiều cao của trống bằng 80 cm. Biết rằng mặt phẳng chứa trục cắt mặt xung quanh của trống là các parabol (như hình vẽ). Hỏi thể tích của trống?
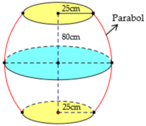
A. 254259,6 c m 3
B. 127129,8 c m 3
C. 80933,3 c m 3
D. 253333,3 c m 3
Tính chiều cao h của khối nón có bán kính đáy bằng 3 và thể tích bằng
36
π
A. h 18 B. h 12 C. h 6 D. h 4
Đọc tiếp
Tính chiều cao h của khối nón có bán kính đáy bằng 3 và thể tích bằng 36 π
A. h =18
B. h =12
C. h =6
D. h =4
Tính thể tích V của khối nón có bán kính đáy bằng 3 và chiều cao bằng 6.
A. 36π
B. 18π
C. 108π
D. 54π