Các câu hỏi tương tự
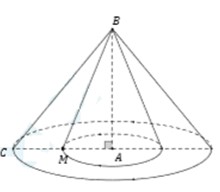
Cho tam giác ABC vuông tại A, cạnh AB=6, AC=8 và M là trung điểm của cạnh AC. Khi đó thể tích của khối tròn xoay do tam giác BMC quanh cạnh AB là
A. 86π
B. 106π
C. 96π
D. 98π
Cho tam giác ABC vuông tại A, cạnh AB = 6, AC = 8 và M là trung điểm của cạnh AC. Khi đó thể tích của khối tròn xoay do tam giác BMC quanh một vòng quanh cạnh AB là
A. 98 π
B. 106 π
C. 96 π
D. 86 π
Tam giác ABC vuông tại B, AB 10, BC 4 . Gọi M,N lần lượt là trung điểm của AB, AC. Thể tích khối tròn xoay do hình thang vuông BMNC quay một vòng quanh MB là: A.
40
π
3
B.
20
π
3
C.
120
π
3
D.
140
π
3
Đọc tiếp
Tam giác ABC vuông tại B, AB = 10, BC = 4 . Gọi M,N lần lượt là trung điểm của AB, AC. Thể tích khối tròn xoay do hình thang vuông BMNC quay một vòng quanh MB là:
A. 40 π 3
B. 20 π 3
C. 120 π 3
D. 140 π 3
Cho tam giác ABC vuông cân tại A,AB2a. Thể tích của khối tròn xoay tạo thành khi quay tam giác ABC quanh cạnh AB bằng A.
π
a
3
3
B.
8
π
a
3
3
C.
4...
Đọc tiếp
Cho tam giác ABC vuông cân tại A,AB=2a. Thể tích của khối tròn xoay tạo thành khi quay tam giác ABC quanh cạnh AB bằng
A. π a 3 3
B. 8 π a 3 3
C. 4 π a 3 3
D. 8 π a 3 2 3
Cho tam giác ABC vuông tại
A
,
AB
6
,
AC
8
.
Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là A.
96
3
π
B.
96
π
C.
384
5
π
D.
1152
5
π
Đọc tiếp
Cho tam giác ABC vuông tại A , AB = 6 , AC = 8 . Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là
A. 96 3 π
B. 96 π
C. 384 5 π
D. 1152 5 π
Cho tam giác ABC vuông tại A,
A
B
6
,
A
C
8
. Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là A.
96
3
π
B.
96
π
C.
384
5
π
D.
1152
5
π
Đọc tiếp
Cho tam giác ABC vuông tại A, A B = 6 , A C = 8 . Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là
A. 96 3 π
B. 96 π
C. 384 5 π
D. 1152 5 π
Tính thể tích của vật thể nằm giữa hai mặt phẳng
x
0
;
x
π
, biết rằng thiết diện của vật thể với mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
∈
0
;
π
là một tam giác đều có cạnh là
2
sin
x
A.
3
B.
π...
Đọc tiếp
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 ; x = π , biết rằng thiết diện của vật thể với mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ∈ 0 ; π là một tam giác đều có cạnh là 2 sin x
A. 3
B. π 3
C. 2 3
D. 2 π
Tam giác ABC vuông tại A, AB a và
A
C
B
^
30
°
. Thể tích khối tròn xoay sinh ra khi quay tam giác ABC quanh cạnh BC bằng c B.
a
3
π
6
C.
3
a
3
π
8...
Đọc tiếp
Tam giác ABC vuông tại A, AB = a và A C B ^ = 30 ° . Thể tích khối tròn xoay sinh ra khi quay tam giác ABC quanh cạnh BC bằng
c
B. a 3 π 6
C. 3 a 3 π 8
D. a 3 π 2
Tính thể tích của vật thể giới hạn bởi hai mặt phẳng
x
0
,
x
π
.
Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ
x
0
≤
x
≤
π
là một tam giác vuông cân có cạnh huyền bằng
sin
x
+
2
A.
7...
Đọc tiếp
Tính thể tích của vật thể giới hạn bởi hai mặt phẳng x = 0 , x = π . Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác vuông cân có cạnh huyền bằng sin x + 2
A. 7 π 6 + 2
B. 7 π 6 + 1
C. 9 π 8 + 2
D. 9 π 8 + 1