Xét △ ADC và △ BEC, ta có:
∠ (ADC) = ∠ (BEC) = 90 0
∠ C chung
Suy ra: △ ADC đồng dạng △ BEC (g.g)
Suy ra: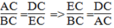 ⇒ ECBC = DCAC
⇒ ECBC = DCAC
Xét △ DEC và △ ABC ta có:
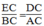
∠ C chung
Vậy △ DEC đồng dạng △ ABC (c.g.c)
Xét △ ADC và △ BEC, ta có:
∠ (ADC) = ∠ (BEC) = 90 0
∠ C chung
Suy ra: △ ADC đồng dạng △ BEC (g.g)
Suy ra: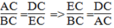 ⇒ ECBC = DCAC
⇒ ECBC = DCAC
Xét △ DEC và △ ABC ta có:
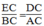
∠ C chung
Vậy △ DEC đồng dạng △ ABC (c.g.c)
Cho tam giác ABC có hai đường cao là AD và BE ( D thuộc BC, E thuộc AC). Chứng minh rằng:
a) tam giác ADC đồng dạng tam giác BEC.
b) AC.EC=BC.DC
c) tam giác DEC đồng dạng tam giác ABC.
Bài: Cho tam giác ABC nhọn với các đường cao AD, BE (D thuộc BC; E thuộc AC). Chứng minh tam giác DEC đồng dạng với tam giác ABC
- Bài này hơi khó, giúp mình nhé, cám ơn !
Câu 1: - cho tam giác ABC . Vẽ MN là đường trung bình của tam giác ABC ( M thuộc AB, N thuộc AC) . Chứng minh tam giác ABC đồng dạng với tam giác AMN
câu 2: cho tam giác ABC có góc A > 90 ( AC > AB) trên cạnh BC, AC lấy 2 điểm D và E sao cho CDE = BAC
A. Chứng minh tam giác ABC đồng dạng tam giác DEC
B. Viết tỉ số đồng dạng cũa tam giác ABC và tam giác DEC
C. Chứng minh DC × BC=EC×AC
Cho tam giác ABC nhọn có ba đường cao AD, BE, CF với D thuộc BC, E thuộc AC, F thuộc AB, Gọi H là trực tâm của tam giác ABC. Chững minh rằng tam giác ABD đồng dạng với tam giác CHD
Cho tam giác ABC vuông tại A có AH là đường cao (H thuộc BC).Biết AB =6cm,Bc=10cm
a,chứng minh rằng tam giác HBA đồng dạng vs tam giác ABC
b,Tính AC,AH,HB
c,I và K lần lượt là hình chiếu của điểmH lên AB, AC. CHứng minh rằng AI .AB=AK.AC
d,Vẽ phân giác của tam giác AD của tam giác ABC ( D thuộc BC).Đường phân giác DE của tam giác ABD(E thuộc AB),đường phân giác DF của tam giác ADC(F thuộc AC) chứng minh rằng EA/EB*DB/DC*FC/FA=1
Cho tam giác ABC có ba góc nhọn, hai đường cao BD và CE của tam giác cắt nhau tại H (D thuộc AC, E thuộc AB)
a) Chứng minh rằng tam giác BHE đồng dạng với tam giác CHD
b) Chứng minh AB.AE = AC.AD
c) Chứng minh góc AED = góc ACB
Cho tam giác ABC vuông tại A (AB<AC) có AH là đường cao (H thuộc cạnh BC).
a, Chứng minh: Tam giác ABC đồng dạng với tam giác HAC và
AC2= BC.HC
b, Gọi CD là tia phân giác góc ACB (D thuộc cạnh AB), E là giao điểm của AH và CD. Chứng minh: AE.AD=HE.BD
Cho tam giác ABC vuông tại A ( AB < AC ), đường cao AH ( H thuộc BC )
1, Chứng minh: Tam giác HBA đồng dạng tam giác ABC và BC2 = BH.BC
2, Kẻ phân giác BE Của góc ABC ( E thuộc AC ), BE cắt AH tại I
Cho tam giác ABC nhọn có đường cao AD và BE. chứng minh tam giác DEC đồng dạng với tam giác ABC