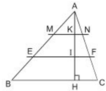
b) SABCD = \(\dfrac{1}{2}\) AH . BC
\(\Rightarrow\) 270 = \(\dfrac{1}{2}\) . AH . 15
\(\Rightarrow\) AH = \(\dfrac{270.2}{15}\) = 36 cm
Ta có AH = 3AK (câu a) và AK = KI (gt)
Do đó AH = 3KI
\(\Rightarrow\) KI = \(\dfrac{AH}{3}\) = \(\dfrac{36}{3}\) = 12 cm
SMNFE = \(\dfrac{1}{2}\) KI (MN + EF) = \(\dfrac{1}{2}\) . 12 (5 + 10) = 90 cm2
a) Ta có AH=AK+KI+IH và AK = KI = IH (gt)
\(\Rightarrow\) AH = 3AK\(\Rightarrow\) \(\dfrac{AK}{AH}\) = \(\dfrac{1}{3}\)
\(\Delta\)ABC có MK // BH (gt) \(\Rightarrow\) \(\dfrac{AM}{AB}\)= \(\dfrac{AK}{AH}\) \(\Rightarrow\) \(\dfrac{AM}{AB}\) = \(\dfrac{1}{3}\)
\(\Delta\)ABC có MN // BC (gt) \(\Rightarrow\) \(\dfrac{MN}{BC}\) = \(\dfrac{AM}{BC}\)
\(\Rightarrow\) \(\dfrac{MN}{BC}\) = \(\dfrac{1}{3}\)
\(\Rightarrow\) \(\dfrac{MN}{15}\)= \(\dfrac{1}{3}\)
\(\Rightarrow\) MN = \(\dfrac{15}{3}\) = 5 cm
...
∆AEI có MK // EI (gt) và K là trung điểm của AI (AK = KI)
\(\Rightarrow\) M là trung điểm của AE
Xét ∆AEF có MN // EF (gt)
\(\Rightarrow\) \(\dfrac{MN}{EF}\) = \(\dfrac{AM}{AE}\)
Mà \(\dfrac{AM}{AE}\) = \(\dfrac{1}{2}\) (M là trung điểm của AE)
Nên \(\dfrac{MN}{EF}\) = \(\dfrac{1}{2}\)
\(\Rightarrow\) \(\dfrac{5}{EF}\) = \(\dfrac{1}{2}\)
\(\Rightarrow\) EF = 10 cm


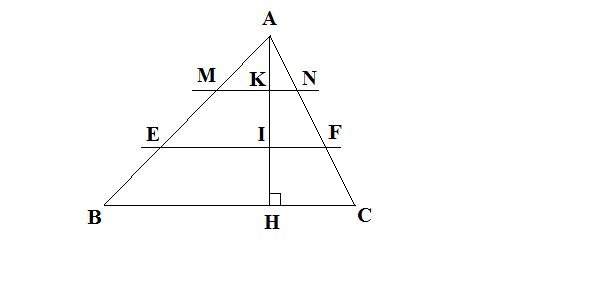 Tam giác ABC có BC = 15cm. Cho AK = KI = IH và EF // BC, MN // BC
Tam giác ABC có BC = 15cm. Cho AK = KI = IH và EF // BC, MN // BC