\(y'=-3x^2+2x-1=-3\left(x-\dfrac{1}{3}\right)^2-\dfrac{2}{3}< 0\) ; \(\forall x\)
\(\Rightarrow\) Hàm nghịch biến trên R
\(\Rightarrow\max\limits_{\left[0;2\right]}y=y\left(0\right)=6\)
\(\min\limits_{\left[0;2\right]}y=y\left(2\right)=0\)
\(y'=-3x^2+2x-1=-3\left(x-\dfrac{1}{3}\right)^2-\dfrac{2}{3}< 0\) ; \(\forall x\)
\(\Rightarrow\) Hàm nghịch biến trên R
\(\Rightarrow\max\limits_{\left[0;2\right]}y=y\left(0\right)=6\)
\(\min\limits_{\left[0;2\right]}y=y\left(2\right)=0\)
Tìm giá trị lớn nhất của hàm số y = f ( x ) = x 3 - 2 x 2 + x - 2 trên đoạn [0;2]
A. ![]()
B. 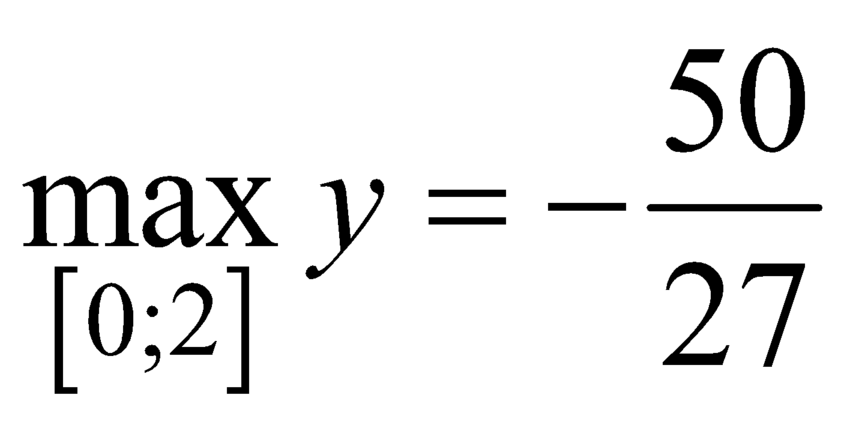
C. ![]()
D. ![]()
Cho hàm số y = f(x) có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số f(x) trên đoạn [0;2] là:
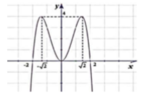
A. M a x [ 0 ; 2 ] f ( x ) = 2
B. M a x [ 0 ; 2 ] f ( x ) = 2
C. M a x [ 0 ; 2 ] f ( x ) = 4
D. M a x [ 0 ; 2 ] f ( x ) = 0
Cho hàm số y = f(x) = | x 4 - 4 x 3 + 4 x 2 + a |. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Số giá trị nguyên a thuộc đoạn [-3;3] sao cho M ≤ 2m là
A. 3
B. 5
C. 6
D. 7
Tìm giá trị lớn nhất của hàm số f ( x ) = x 3 - 2 x 2 + x - 2 trên đoạn [0;2].
![]()
![]()
![]()
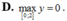
Ký hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;2]. Giá trị a+A bằng
![]()
![]()
![]()
![]()
Ký hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;2]. Giá trị của a+A bằng
A. 19 3
B. 22 3
C. 7
D. 12
Cho hàm số f(x) = | x 4 - 4 x 3 + 4 x 2 + a |. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-3;2] sao cho M ≤ 2m?
A. 7
B. 5
C. 6
D. 4
Cho hàm số f(x), đồ thị hàm số y=f '(x) là đường cong trong hình bên. Giá trị lớn nhất của hàm số g(x) = -f(2x-1) +2x trên đoạn [0;2] bằng
Giá trị nhỏ nhất của hàm số f ( x ) = x 2 + x + 4 x + 1 trên đoạn [0;2] bằng
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) nghịch biến trên ℝ và thỏa mãn [f(x) - x]f(x) = x 6 + 3 x 4 + 2 x 2 , ∀ x ∈ ℝ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng
A. 4
B. -28
C. -3
D. 33