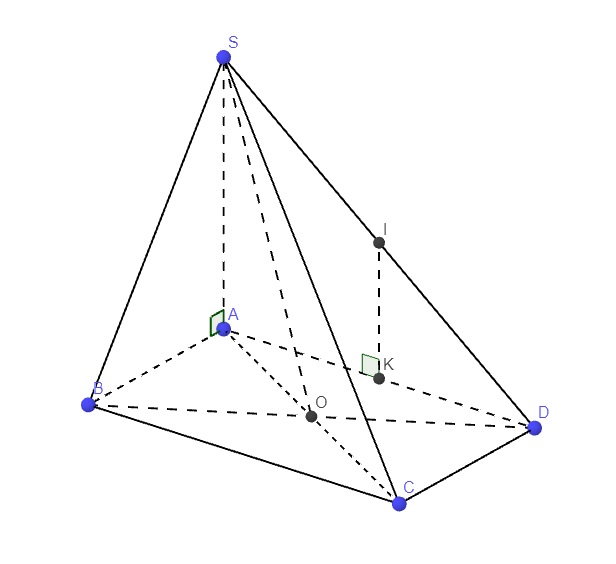
a) Ta có:
`SA⊥(ABCD) ⇒ SA⊥AO`
⇒ `AO` là hình chiếu của `SO` lên `(ABCD)`
⇒ `∠(SO;(ABCD))=∠(SO;AO)=∠SOA=45^o`
`AC=\sqrt{AB^2+BC^2}=\sqrt{a^2+3a^2}=2a`
⇒ `AO=\frac{AC}{2}=a/2`
`SA=AO\tanSOA=a\tan45^o=a`
Vậy `V_{S.ABCD}=\frac{1}{3}SA.ABCD=\frac{1}{3}a.a.a\sqrt{3}=\frac{a^3\sqrt{3}}{3}`
b) `S_{ΔOCD}=\frac{1}{2}.\frac{1}{2}BC.AB=\frac{1}{4}.a\sqrt{3}.a=\frac{a^2\sqrt{3}}{4}`
`V_{S.OCD}=\frac{1}{3}SA.S_{ΔOCD}=\frac{1}{3}.a.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{12}`
c) Kẻ $IH \ // \ SA \ (H∈AD) ⇒ IH⊥(ABCD)$
Hay `IH⊥(OBC)`
Ta có:
`S_{ΔOBC}=\frac{1}{2}.\frac{1}{2}AB.BC=\frac{1}{4}.a.a\sqrt{3}=\frac{a^2\sqrt{3}}{4}`
Vì `I` là trung điểm của `SD` nên `IH=\frac{SA}{2}=a/2`
Vậy `V_{I.OBC}=\frac{1}{3}IH.S_{ΔOBC}=\frac{1}{3}.\frac{a}{2}.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{24}`

\(AC=\sqrt{AB^2+BC^2}=2a\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(\Rightarrow\widehat{SOA}=45^0\)
\(\Rightarrow SA=AO.tan45^0=a\)
a.
\(V=\dfrac{1}{3}.SA.AB.BC=...\)
b.
\(S_{\Delta OCD}=\dfrac{1}{4}S_{ABCD}=\dfrac{1}{4}AB.BC=\dfrac{a^2\sqrt{3}}{4}\)
\(\Rightarrow V_{S.OCD}=\dfrac{1}{3}SA.S_{\Delta OCD}=...\)
c.
Gọi K là trung điểm AD \(\Rightarrow IK\) là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}IK||SA\Rightarrow IK\perp\left(OBC\right)\\IK=\dfrac{1}{2}SA=\dfrac{a}{2}\end{matrix}\right.\)
\(S_{\Delta OBC}=\dfrac{1}{4}S_{ABCD}=\dfrac{a^2\sqrt{3}}{4}\)
\(\Rightarrow V_{IOBC}=\dfrac{1}{3}IK.S_{\Delta OBC}=...\)