\(a,A=\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}+...+\dfrac{1}{5^{2025}}\)
\(5A=1+\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{2024}}\)
\(5A-A=\left(1+\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{2024}}\right)-\left(\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}+...+\dfrac{1}{5^{2025}}\right)\)
\(4A=1+\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{2024}}-\dfrac{1}{5}-\dfrac{1}{5^2}-\dfrac{1}{5^3}-...-\dfrac{1}{5^{2025}}\)
\(4A=1-\dfrac{1}{5^{2025}}\)
\(A=\dfrac{1-\dfrac{1}{5^{2025}}}{4}\)
`C = 1/(1.2.3) + ... + 1/(18.19.20)`
`=> 2C = 2/(1.2.3) + ... + 2/(18.19.20)`
`=> 2C = 1/(1.2) - 1/(2.3) + ... + 1/(18.19) - 1/(19.20)`
`=> 2C = 1/2 - 1/380`
`=> 2C= 189/380`
`=> C = 189/380 : 2`
`=> C = 189/760`
Vậy `C = 189/760`

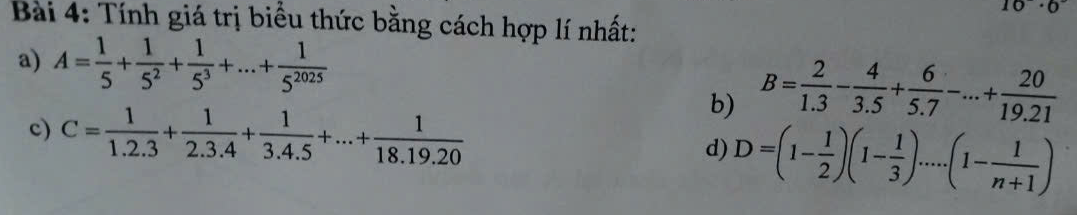






 SOS
SOS